Grundlagen zu Oberflächenrauheit

Autoren: Victoria Marcune,Shawn Iles

Die Oberflächenrauheit beschreibt eine Abweichung der Oberfläche von ihrer idealen Form, wobei höhere Werte raueren Oberflächen entsprechen, während niedrigere Werte eine glatte Oberfläche anzeigen. Die Rauheit bezieht sich auf Fehler mit hoher Ortsfrequenz, d. h. auf sehr kleine Abweichungen in der Größenordnung von Angström (10^-10 m). Das Verständnis der Oberflächenrauheit optischer Oberflächen ist entscheidend für die Kontrolle der Lichtstreuung, da sich die Streuung proportional zur Oberflächenrauheit der Optik verhält. Lichtstreuung und -absorption durch Oberflächenrauheit haben zum Beispiel einen erheblichen Einfluss auf Hochleistungslasersysteme und wirken sich negativ auf die Effizienz und die Laserzerstörschwelle aus. Die Streustrahlung von Hochleistungslasern hat aber nicht nur Auswirkungen auf die Zerstörschwelle, sondern kann auch ein Sicherheitsrisiko für alle Personen in der Nähe des Systems darstellen, da das Licht in unbeabsichtigte Richtungen umgelenkt wird. Die derzeitige Norm für die Oberflächenrauheit ist die ISO 10110-8, welche definiert, wie die Oberflächenrauheit analysiert und spezifiziert werden sollte.

Spezifikation der Oberflächenrauheit verstehen

Eine Zeichnung nach ISO 10110-8 enthält die folgenden Spezifikationen, um eine vollständige Beschreibung der optischen Oberfläche zu ermöglichen.

Abbildung 1: Beispielhafte Spezifikation der Oberflächenrauheit

Oberflächengüte, in Abbildung 1 als "P3" dargestellt:

Dieser Wert gibt die Oberflächenbeschaffenheit an. Bei der Angabe kann es sich entweder um ein G für eine geschliffene Oberfläche oder um ein P für eine optisch polierte Oberfläche handeln. Der Politurgrad wird von 1-4 je nach Grad der Glätte in Form von Mikrodefekten pro 10-mm-Scan eingestuft, wie in Tabelle 1 dargestellt:

Politurgrad	Anzahl N der Mikrodefekte pro 10 mm Probenlänge
P1	80 ≤ N < 400
P2	16 ≤ N < 80
P3	3 ≤ 16
P4	N < 3

Tabelle 1: Angabe des Politurgrades in Form von Mikrodefekten

Verwendete statistische Methode, in Abbildung 1 als "Rq 4" angegeben:

Hier wird die statistische Methode zur Messung der Oberflächenrauheit angegeben, gefolgt von dem Wert.

Räumliche Bandbreite, in Abbildung 1 als "1/0,003" dargestellt:

Hier wird die räumliche Bandbreite angegeben, die von der oberen bis zur unteren Grenze reicht.

Raumfrequenzen und Frequenzgruppen

Bei der Beschreibung der Oberfläche einer optischen Komponente ist es wichtig, den Bereich der räumlichen Auflösung zu definieren. Die Oberflächenbeschaffenheit kann in drei Hauptgruppen von Raumfrequenzen unterteilt werden: Rauheit, Welligkeit und Form.

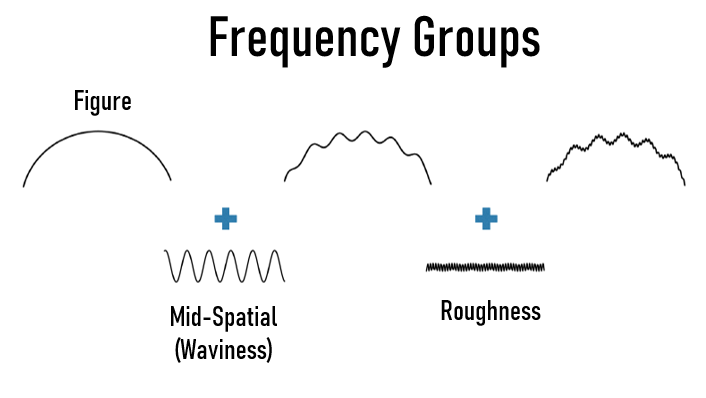
Abbildung 2: Form, Welligkeit und Rauheit charakterisieren die Oberflächentextur in verschiedenen Maßstäben

Abbildung 2 zeigt, wie Oberflächenform, Welligkeit und Rauheit zusammen alle Abweichungen einer Oberfläche von ihrer idealen Form charakterisieren. Die Form beschreibt die Gesamtform der Oberfläche. Es handelt sich um den größten Maßstab bzw. die größten räumlichen Frequenzen, die analysiert werden sollen. Die durch die Form beschriebenen Fehler liegen in der Größenordnung von Zehntelmillimetern bis -zentimetern. Die Welligkeit misst Fehler mit mittlerer räumlicher Frequenz und beschreibt Merkmale in der Größenordnung von µm bis mm. Die Rauheit ist die kleinste Fehlerform und beschreibt eng beieinander liegende Anomalien in der Oberflächenstruktur in der Größenordnung von Zehntelangström bis zu einigen µm.

Oberflächenrauheitsparameter nach ISO 10110-8

Ziel der ISO 10110-8 ist es, Regeln für die Definition der Oberflächenbeschaffenheit festzulegen. Laut ISO ist die „Oberflächentextur das Merkmal einer Oberfläche, das mit statistischen Methoden effektiv beschrieben werden kann". Die ISO-Norm beschreibt 5 statistische Methoden, die zur Beschreibung optisch glatter Oberflächen verwendet werden. Diese Methoden können kombiniert und auch in verschiedenen räumlichen Bandbreiten eingesetzt werden. Die Festlegung der oberen und unteren Grenzen der Raumfrequenz ist entscheidend für die Erzielung akkurater Ergebnisse. Wenn keine Ortsfrequenz definiert ist, wird in der Norm ISO 10110-8 ein Bereich von 0,0025 mm bis 0,08 mm angenommen.

1. & 2. RMS-Rauheit und -Welligkeit: In den USA ist die Methode des quadratischen Mittelwerts (root mean square, RMS) die gängigste Methode, um optisch glatte Oberflächen zu spezifizieren, während es in Europa üblicher ist, die absolute Rauheit anzugeben. Der RMS-Mittelwert der Profilhöhenabweichungen von der Mittellinie wird zur statistischen Analyse der Glätte einer optischen Oberfläche verwendet. RMS-Rauheit, $ Rq $, bezieht sich auf das Rauheitsprofil, während sich die RMS-Welligkeit, $ Wq $, auf das Welligkeitsprofil bezieht. Beide werden mit der gleichen RMS-Methode gemessen, jedoch über unterschiedliche Raumfrequenzbereiche.

$$ \{ Rq, Wq \} \in T $$

$$ T = \sqrt{\frac{1}{lr} \int_0^{lr} Z^2 \! \left(x \right) \text{d} x} $$

Wobei gilt:

$ Rq $: Oberflächenrauheit (RMS-Abweichung)

$ Wq $: Oberflächenwelligkeit (RMS-Abweichung)

$ T $: Allgemeine Oberflächentextur (Rauheit oder Welligkeit; RMS-Abweichung)

$ lr $: Länge der Probe

$ Z \! \left( x \right) $: Oberflächenprofil entlang der x-Achse

Beispiel für ein Rauheitsprofil, das über eine bestimmte Abtastlänge gemessen wurde. Rq<sup>2</sup> gibt die RMS-Höhe an.

Abbildung 3: Beispiel für ein Rauheitsprofil, das über eine bestimmte Abtastlänge gemessen wurde. Rq² gibt die RMS-Höhe an.

3. RMS-Steigung: Ähnlich wie durch die RMS-Rauheit und -Welligkeit können optisch glatte Oberflächen auch durch die RMS-Steigung der lokalen Neigung der Oberfläche entlang einer bestimmten Abtastlänge, $ \tfrac{\text{d} Z \left( x \right)}{\text{d}x} $, spezifiziert werden.

$$ \Delta T = \sqrt{ \frac{1}{lr} \int_0 ^{lr} \left[ \frac{\text{d} Z \! \left( x \right) }{\text{d} x} \right]^2 \text{d}x } $$

$$ \begin{pmatrix} T\\ T \Delta q \end{pmatrix} = \begin{Bmatrix} \begin{pmatrix} Rq\\ R \Delta q \end{pmatrix} \text { für } 1 \large{\unicode[computer modern]{x212B}} \leq lr\leq 1 \large{\unicode[computer modern]{x03BC}} \normalsize{\text{m}} \\ \begin{pmatrix} Wq\\ W \Delta q \end{pmatrix} \text { für } 1 \large{\unicode[computer modern]{x03BC}} \normalsize{\text{m}} < lr\leq 1 \text{mm} \end{Bmatrix} $$

$$ \Delta T = \sqrt{ \frac{1}{lr} \int_0 ^{lr} \left[ \frac{\text{d} Z \! \left( x \right) }{\text{d} x} \right]^2 \text{d}x } $$

(Scrollen Sie nach rechts, um die vollständige Gleichung zu sehen.)

Wobei gilt:

$ R \Delta q $: Steigung der Oberflächenrauheit (RMS-Steigung)

$ W \Delta q $: Steigung der Oberflächenwelligkeit (RMS-Steigung)

4. Angabe der Dichte der Mikrodefekte: Als Mikrodefekte werden die Vertiefungen und Kratzer bezeichnet, die auf einer optisch glatten Oberfläche zu finden sind. Sie werden in der Regel mit einem optischen Profilometer, einem Mikroskop oder einem mikroskopischen Bildkomparator quantifiziert. In ISO 10110-8 heißt es: "Die Anzahl der Mikrodefekte $ N $ wird über einen 10-mm-Zeilenscan mit einer Auflösung von 3 µm oder über eine Fläche von 300 µm x 300 µm mit der gleichen Auflösung bestimmt."

5. Funktion der spektralen Leistungsdichte (PSD): Die PSD-Funktion ist eine der umfassendsten statistischen Methoden zur Messung der Oberflächenrauheit. Sie ermöglicht eine vollständige Beschreibung der Oberflächentexturmerkmale, indem sie die relative Stärke jeder Rauheitskomponente als Funktion der Raumfrequenz angibt.

$$ \text{PSD} \! \left( f_x, f_y \right) = \lim_{L \to \infty} \frac{1}{L^2} \left| \int_{-L/2}^{L/2} \int_{-L/2}^{L/2} z \! \left( x, y \right) \exp{ \left[ -2 \pi j \left( f_x x + f_y y \right) \right] } \text{d} x \text{d} y \right| $$

(Scrollen Sie nach rechts, um die vollständige Gleichung zu sehen.)

Dies ist die allgemeine Gleichung zur Berechnung der PSD einer 2-dimensionalen Fläche. $ f_x $ und $ f_y $ sind die Ortsfrequenzen der Oberflächenstruktur $ z \! \left( x, y \right) $, die über eine quadratische Fläche der Seitenlänge $ L $ definiert ist.

Messtechnik zur Messung der Oberflächenrauheit

Es gibt eine Reihe von Messtechniken, die für unterschiedliche Raumfrequenzen besonders geeignet sind. Die gängigsten sind die konventionelle Interferometrie, die Weißlichtinterferometrie und die Rasterkraftmikroskopie. Abbildung 4 zeigt, für welche Regionen und Wellenlängen die einzelnen Verfahren am besten eingesetzt werden können.

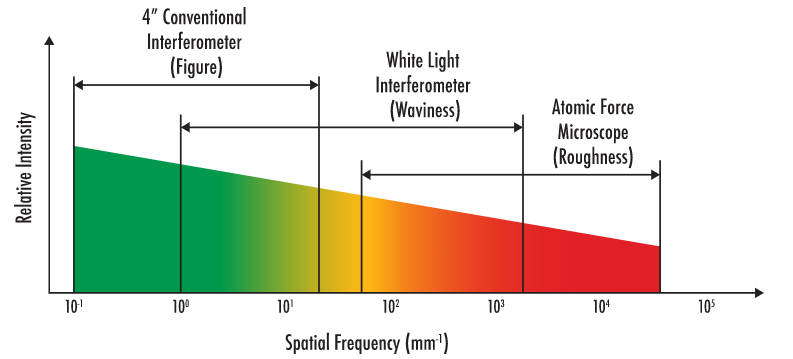
Abbildung 4: Räumlicher Frequenzbereich typischer Messgeräte.

Die herkömmliche Interferometrie ist ideal für die Messung von Fehlern mit niedriger Ortsfrequenz. Diese Klasse von Oberflächenfehlern wird als Formfehler bezeichnet und steht mit typischen Zernike-Polynomen im Zusammenhang. Zernike-Polynome beschreiben Fehler, die durch Wellenfrontaberrationen verursacht werden, wenn eine optische Komponente von einer idealen Form abweicht. Ein Weißlichtinterferometer eignet sich am besten zur Messung von Welligkeit oder Fehlern im mittleren Bereich der Raumfrequenz. Welligkeit wird oft für Effekte wie Trübung und verminderten Kontrast verantwortlich gemacht. Schließlich bietet das Rasterkraftmikroskop die beste Auflösung für hochfrequente räumliche Fehler, die die Rauheit der optischen Oberfläche charakterisieren. Zwischen den Bereichen gibt es einige Überschneidungen, sodass sowohl das Weißlichtinterferometer als auch das Rasterkraftmikroskop zur Messung der Rauheit verwendet werden können. Die Wahl des richtigen Geräts hängt teilweise auch von der Wellenlänge der Anwendung ab. Weißlichtinterferometrie ist beispielsweise ideal für die Messung von VIS- oder IR-Spektren, da diese in der Regel bei Frequenzen von weniger als 2.000 Zyklen/mm analysiert werden.

Spezifikation der Oberflächenqualität für Ultrakurzpulsoptiken

Bei der Analyse von Ultrakurzpulsoptiken müssen die Hersteller die Oberflächenqualität nach eigenem Ermessen festlegen, da derzeit keine gültige Norm vorliegt. Einige Hersteller von Ultrakurzpulsoptiken geben z. B. nur die Oberflächenqualität vor der Beschichtung an, während andere Hersteller eine Qualität von 20-10 oder höher nach der Beschichtung angeben.

Optiken, die für Ultrakurzpuls-Anwendungen entwickelt werden, weisen in der Regel dicke, spezielle Beschichtungen auf, die einen langen Sputter-Prozess erfordern. Aufgrund der Länge dieses Prozesses können Unregelmäßigkeiten in die Beschichtung „gesputtert“ werden, was den Eindruck von "Staub" oder einer schlechteren Oberflächenqualität erzeugen kann. Diese Unregelmäßigkeiten entstehen aber nicht durch Staub, sondern durch kleine Schwankungen im Fluss des gesputterten Materials. Diese Schwankungen der Sputter-Rate während des Beschichtungsprozesses können zu lokalen Mikroablagerungen in der Beschichtung führen.

Typisches Aussehen einer Optik mit einer Ultrakurzpulsbeschichtung. Trotz der scheinbar unregelmäßigen Oberflächenqualität garantiert Edmund Optics die spezifizierte Leistung seiner Ultrakurzpulsoptiken.

Abbildung 5: Typisches Aussehen einer Optik mit einer Ultrakurzpulsbeschichtung. Trotz der scheinbar unregelmäßigen Oberflächenqualität garantiert Edmund Optics die spezifizierte Leistung seiner Ultrakurzpulsoptiken.

Obwohl sie gut sichtbar sind, haben diese Mängel nur geringfügige Auswirkungen auf die Gesamtleistung der Optik. Aufgrund der relativ geringen Größe dieser Unregelmäßigkeiten sind die betroffenen Strahlteile unbedeutend, wenn man die Eigenschaften des Films wie Gruppenlaufzeitdispersion und Reflexionsvermögen berücksichtigt. Allerdings kann es bei Anwendungen, die kleine Strahlgrößen oder extrem niedrige Verluste erfordern, zu einer Zunahme der Streuung durch das System aufgrund dieser Unregelmäßigkeiten kommen. Um engere Spezifikationen zu erreichen, können besondere Maßnahmen ergriffen werden, welche die Gesamtstreuung verringern, z. B. kann die Fertigung mit einem hochglanzpolierten Substrat begonnen werden.

Messtechnik bei Edmund Optics^®

Die Vermessung der hergestellten Produkte ist ein wichtiger Bestandteil der Produktion. Edmund Optics wendet ein strenges globales Qualitätssicherungsprogramm an, um sicherzustellen, dass die Komponenten die spezifizierten Anforderungen erfüllen. Eine Reihe von Geräten, darunter Interferometer, Profilometer, Koordinatenmessgeräte (CMM) und eine Vielzahl anderer optischer und mechanischer Messgeräte, werden zur Durchführung hausinterner Tests zur Bestimmung der Oberflächenrauheit und anderer optischer Eigenschaften eingesetzt. Weitere Informationen zu kundenspezifischen Messtechniken finden Sie auf unserer Webseite Testen & Messen.

Literatur

ISO 10110-8:2019, Optics and photonics — Preparation of drawings for optical elements and systems — Part 8: Surface texture
Filhaber, John. “LARGE OPTICS: Mid-Spatial-Frequency Errors: The Hidden Culprit of Poor Optical Performance.” Laser Focus World, 13 Aug. 2013
“Root Mean Square Slope (Rδq, Pδq, Wδq): Surface Roughness Parameters.” Root Mean Square Slope (Rδq, Pδq, Wδq) | Surface Roughness Parameters | Introduction To Roughness | KEYENCE America
Deck, Leslie L., and Chris Evans. “High Performance Fizeau and Scanning White-Light Interferometers for Mid-Spatial Frequency Optical Testing of Free-Form Optics.” Advances in Metrology for X-Ray and EUV Optics, 2005, https://doi.org/10.1117/12.616874.
Jayson Nelson, Shawn Iles, "Creating sub angstrom surfaces on planar and spherical substrates," Proc. SPIE 11175, Optifab 2019, 1117505 (15 November 2019); https://doi.org/10.1117/12.2536689