Tunnel-Diagramme für Prismen

Prismen werden eingesetzt, um optische Wege umzulenken, die Ausrichtung und Größe von Abbildungen zu verändern und um Licht zu beugen. In vielen Anwendungen werden Kombinationen von Prismen eingesetzt, um mehrere dieser Effekte zu erzielen. Wenn Baugruppen entwickelt werden, die verschiedene Prismen enthalten, ist es wichtig zu verstehen, wo Licht in die Prismen eintritt, sich ausbreitet und die Prismen wieder verlässt und es kann auch hilfreich sein, die optische Weglänge des Lichts im Prisma zu kennen. Dies alles kann einfach über Tunnel-Diagramme für Prismen modelliert werden.

Ein Tunnel-Diagramm für Prismen ist eine zweidimensionale (2D) Zeichnung, die den Weg eines Strahls durch ein Prisma darstellt¹ und den Strahlengang visualisiert. In solch einem Diagramm wird ein maßstabsgetreuer Querschnitt des Prismas gezeigt. Ein Strahl beginnt außerhalb des Prismas und tritt durch eine der Flächen ein. Im Prisma trifft der Strahl auf andere Prismenflächen. Wenn der Strahl in einem Winkel gleich oder größer als der kritische Winkel (dieser hängt von den Brechungsindizes der Medien ab) auf eine neue Oberfläche trifft oder wenn diese Oberfläche mit einer entsprechenden Spiegelbeschichtung versehen ist, entsteht eine totale interne Reflexion bzw. eine nahezu totale interne Reflexion. Wird der Strahl von einer Fläche reflektiert, wird der Querschnitt des Prismas über die Linie, die die reflektierende Fläche darstellt, gekippt, sodass es aussieht, als würde der Strahl geradeaus durch den nächsten Prismenquerschnitt laufen, ohne seine ursprüngliche Richtung zu ändern. Trifft der Strahl in einem Winkel, der nicht größer oder gleich dem kritischen Winkel ist, auf eine Fläche ohne Spiegelbeschichtung, tritt er durch diese Oberfläche aus dem Prisma aus. Ein Beispiel eines Tunnel-Diagramms für ein Pentaprisma ist in Abbildung 1 gezeigt zusammen mit einem typischen Strahlengangdiagramm.

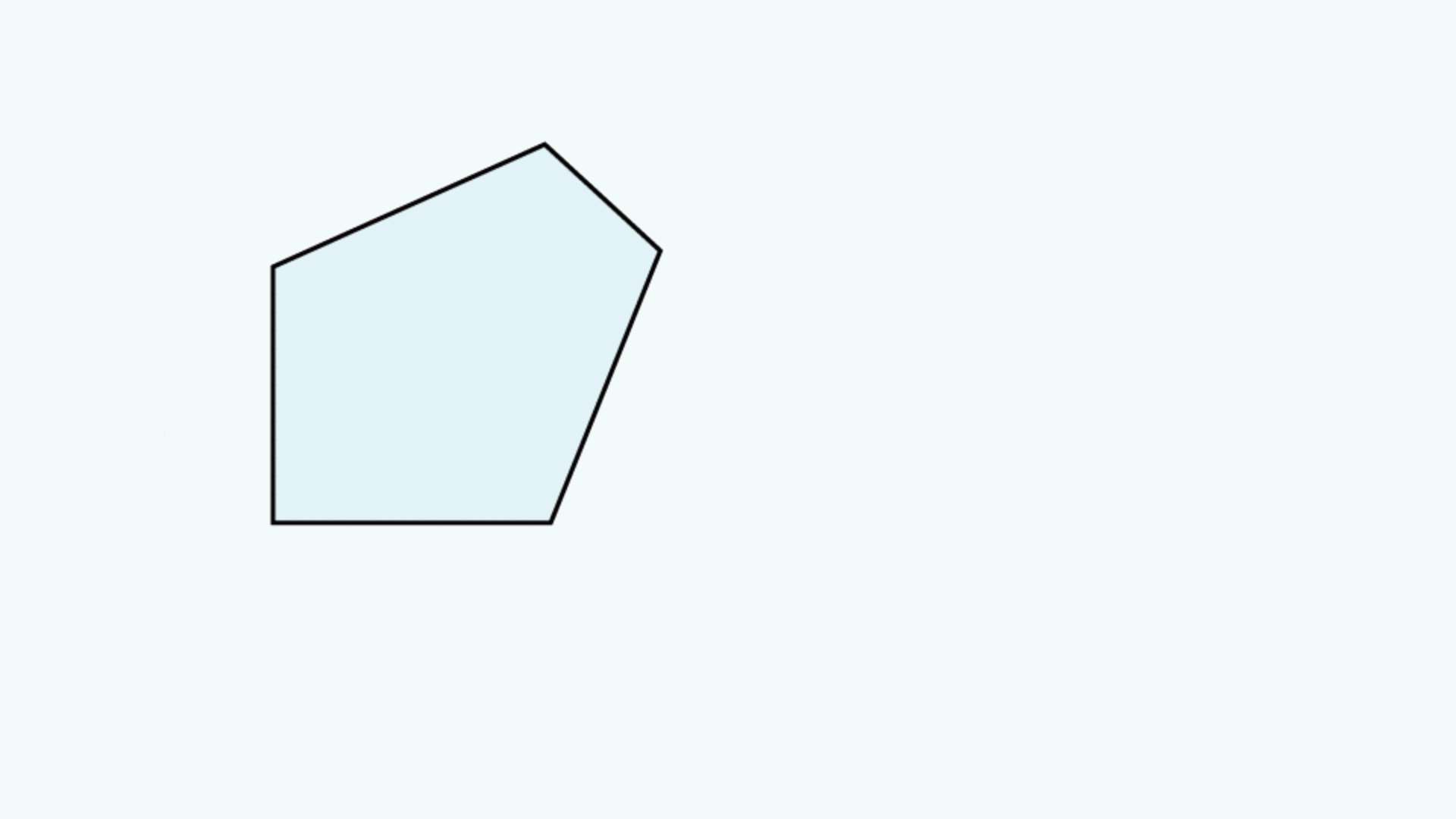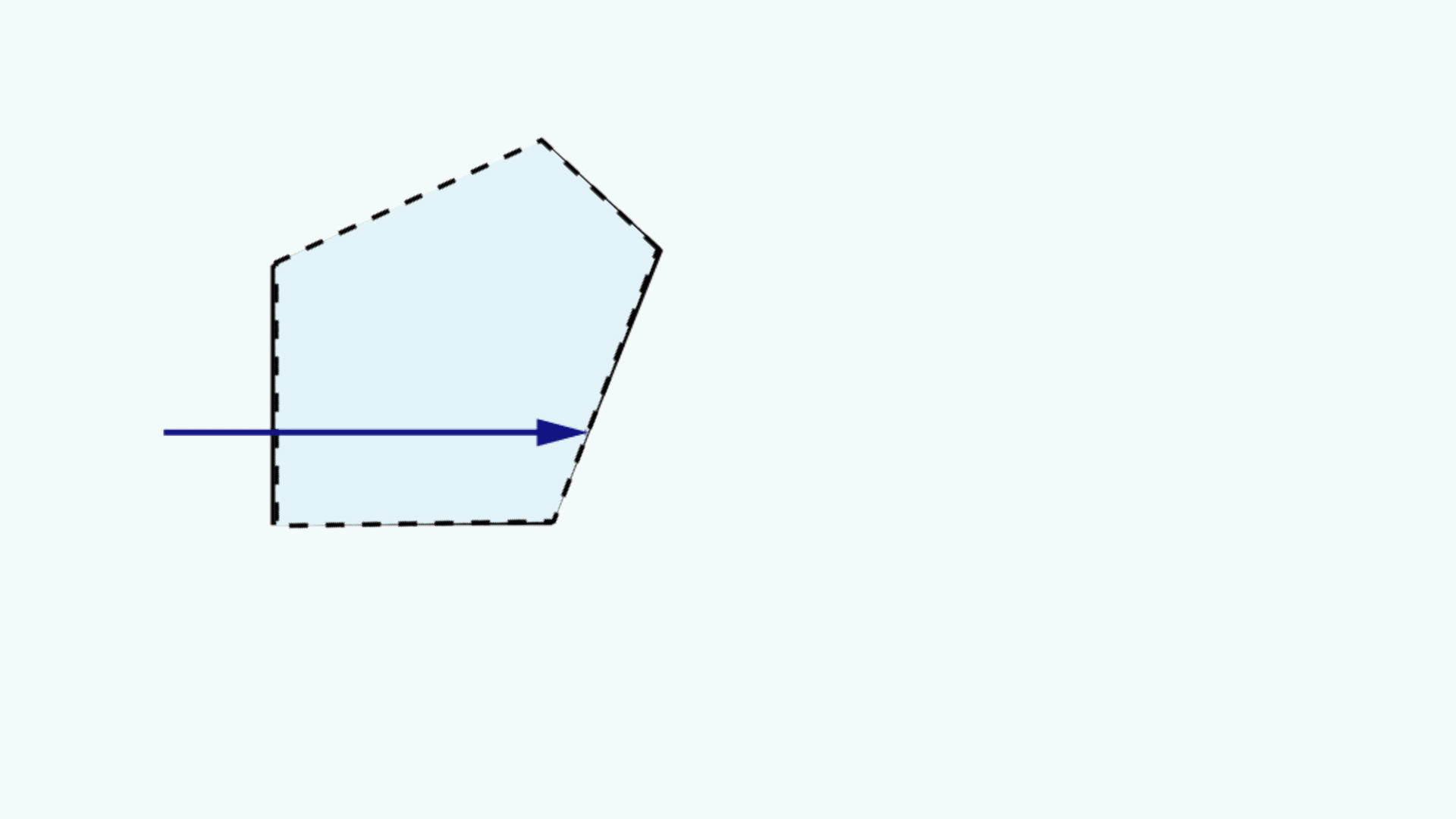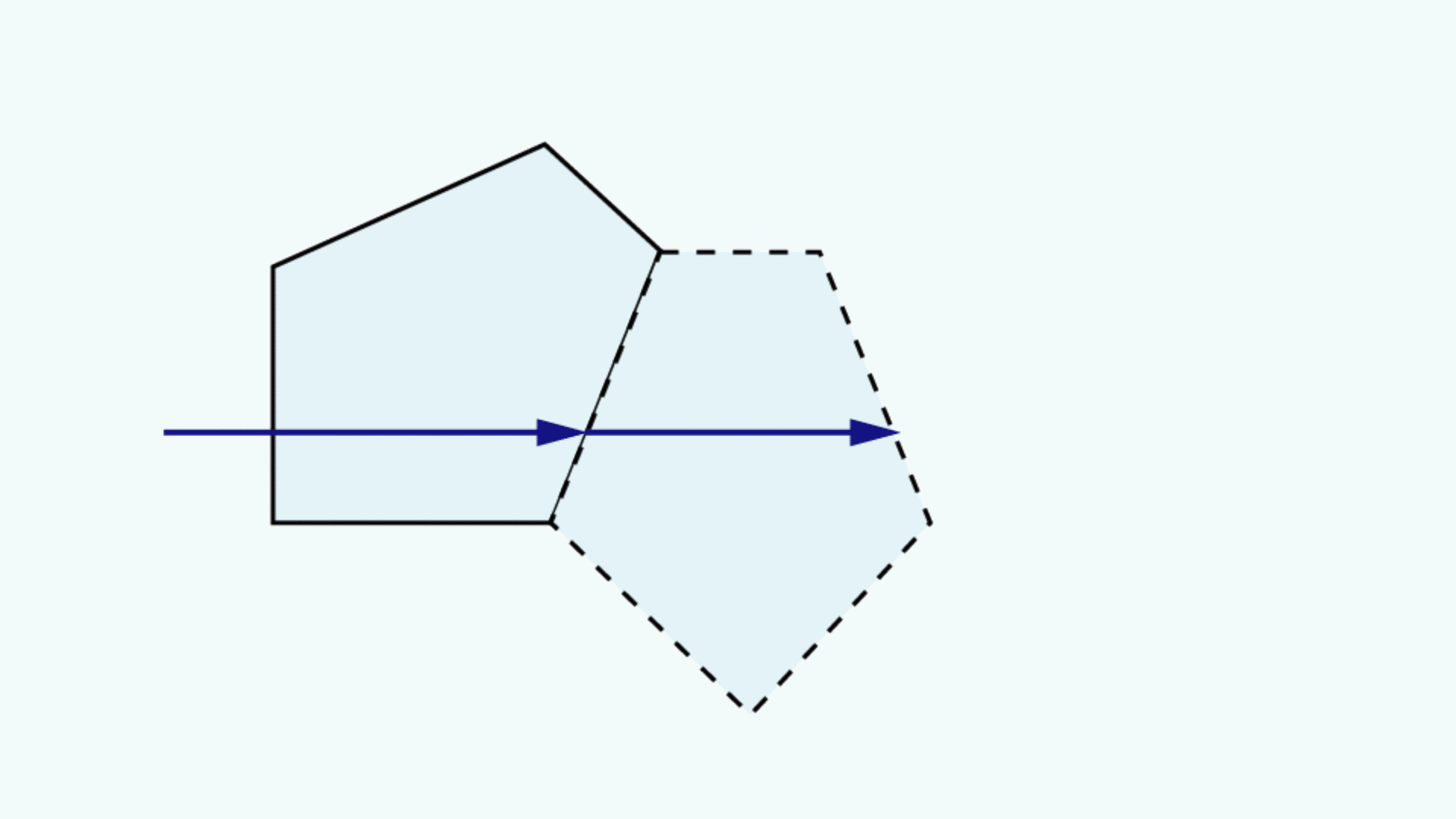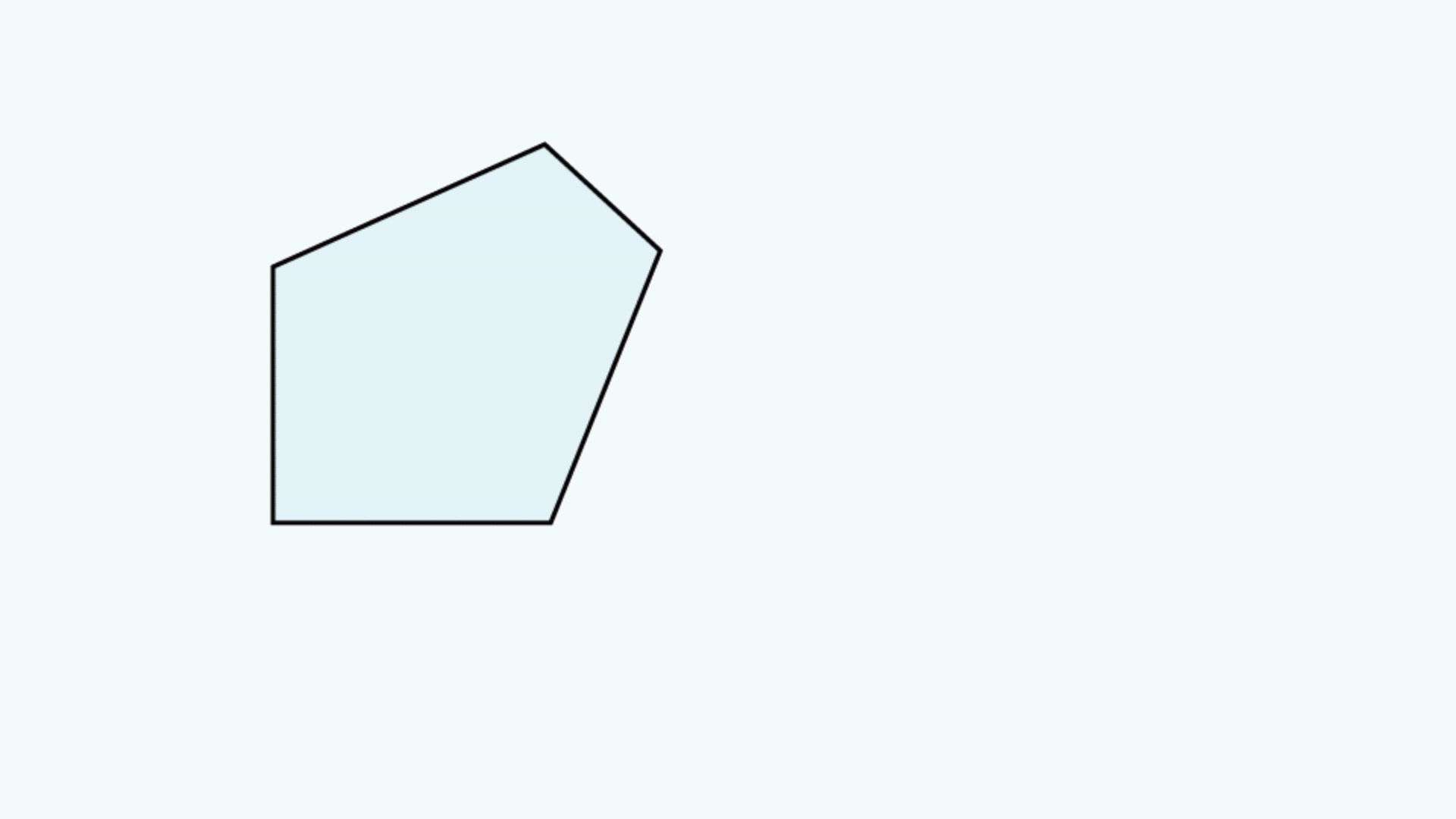
Abbildung 1: Oben: Typisches Strahlengangdiagramm für ein Pentaprisma. Unten: Tunnel-Diagramm des Strahlengangs durch das gleiche Pentaprisma.

Mithilfe eines Tunnel-Diagramms lässt sich die freie Apertur eines Prismas ermitteln und verdeutlichen, wo eine Vignettierung auftritt, die das Sichtfeld des Prismas beeinflusst. Es können mehrere Tunnel-Diagramme für verschiedene Strahlengänge durch ein Prisma gezeichnet werden. Für den Strahleintritt durch verschiedene Flächen und in verschiedenen Winkeln können jeweils einzelne Diagramme erstellt werden. So werden zum Beispiel Doveprismen häufig in verschiedenen Ausrichtungen verwendet, um unterschiedliche Bildtransformationen zu erreichen. Jeder dieser verschiedenen Strahlengänge durch ein Prisma hat ein anderes Tunnel-Diagramm (siehe Tabelle 1). 
 

2D-Strahlengangdiagramm	Entsprechendes Tunnel-Diagramm

Tabelle 1: Tunnel-Diagramme für Doveprismen

Bei dem oberen und unteren Diagramm tritt der Lichtstrahl an den gleichen Flächen ein und aus, aber die Eintritts- und Austrittswinkel sind unterschiedlich. Außerdem gibt es beim ersten Diagramm nur eine reflektierende Oberfläche, beim zweiten und dritten aber zwei bzw. drei Reflexionen.

In 2D-Strahlengangdiagrammen wird ein „V“ an einer Dachfläche oder einem Bereich, in dem zwei Flächen des Prismas einen 90° Winkel und somit eine „dachförmige“ Form bilden, hinzugefügt (Abbildung 2).² Hier entsteht eine zusätzliche Reflexion und die Bildausrichtung wird verändert.

Abbildung 2: In der 2D-Zeichnung wird ein „V“ hinzugefügt, damit die Dachfläche des Amiciprismas von anderen Flächen unterschieden werden kann.

Geringerer Abstand

Bei Licht, das durch eine planparallele Platte fällt, wird aufgrund der Beugung ein Bildversatz auftreten (Abbildung 3). Dieser Bildversatz ist eine Funktion der Plattendicke (t) und des Brechungsindex (n).

Abbildung 3: Bildversatz verursacht durch eine planparallele Platte.

Bei einem Bildversatz durch das Glas muss dann statt der eigentlichen Weglänge die reduzierte Entfernung verwendet werden. Um die reduzierte Weglänge zu berechnen, wird die eigentliche Weglänge im Glas (L) durch n geteilt.² Dieser Wert wird auch häufig in Tunnel-Diagrammen für Prismen verwendet, um die luftäquivalente Weglänge durch das Prisma zu bestimmen (Abbildung 3).

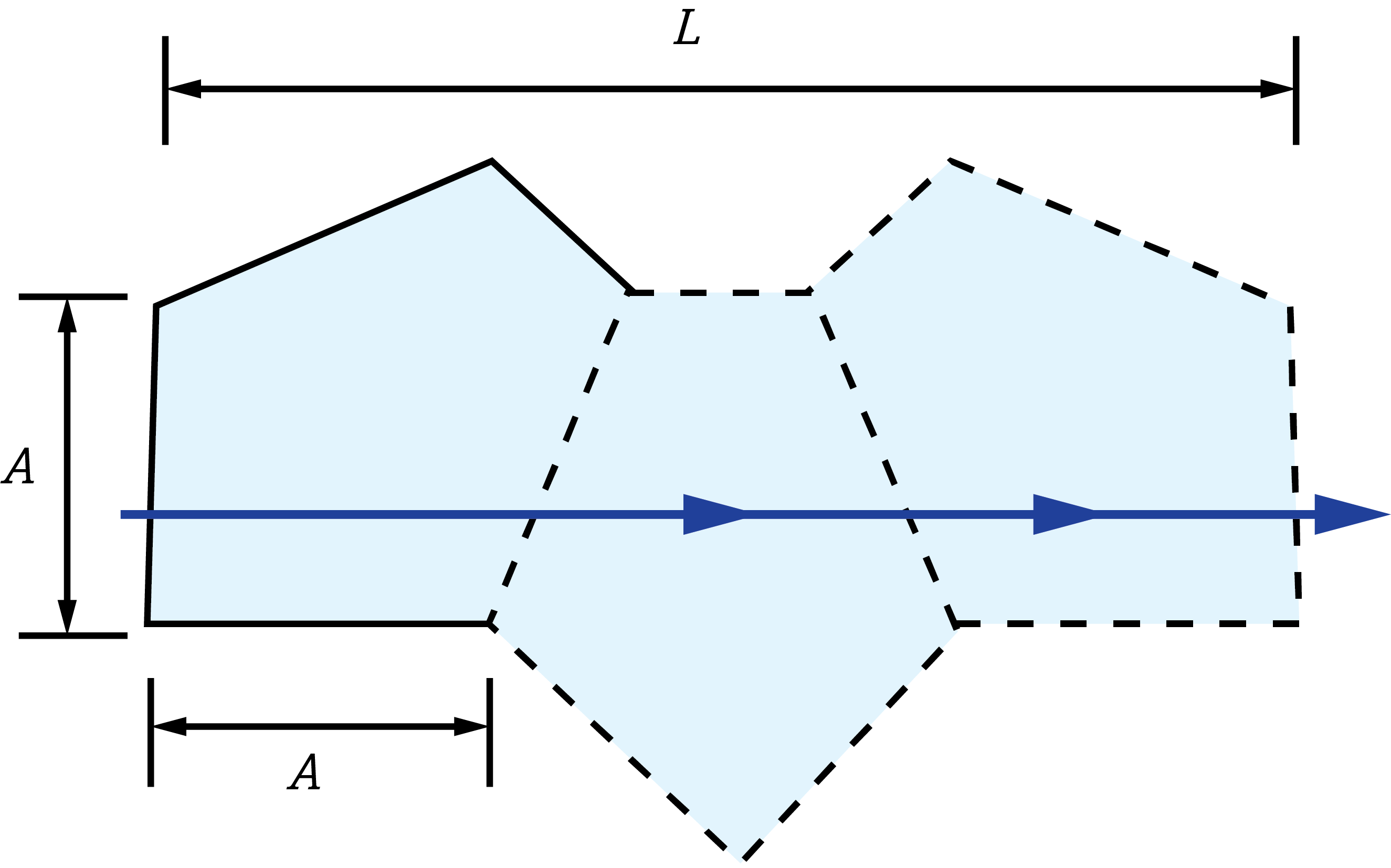
Abbildung 4: Tunnel-Diagramm eines Pentaprismas mit reduzierter Weglänge.

Tunnel-Diagramme für übliche Prismentypen

Unten finden Sie eine Sammlung von aufgefalteten Tunnel-Diagrammen für übliche Prismentypen. Die verwendete optische Weglänge ist die wirkliche Entfernung, die das Licht im Prisma zurücklegt, nicht die reduzierte. Um die reduzierte Entfernung zu bestimmen, muss die optische Weglänge durch den Brechungsindex des Prismas geteilt werden.

Rechtwinklige Prismen:

Strahlablenkung um 90° oder 180° Erzeugen seitenverkehrte Bilder aufgrund einer einzigen Reflexion Können kombiniert werden, um Bild-/Strahlversatz zu erzeugen Produkte ansehen

3D-Strahlengangdiagramm	2D-Strahlengangdiagramm	Entsprechendes Tunnel-Diagramm	Optische Weglänge
			$$ A $$
			$$ A $$

Littrowdispersionsprismen:

Strahlablenkung um 60°, wenn beschichtet Erzeugen seitenrichtiges Bild Teilen Licht ohne Reflexion in seine spektralen Komponenten auf, wenn unbeschichtet Produkte ansehen

3D-Strahlengangdiagramm	2D-Strahlengangdiagramm	Entsprechendes Tunnel-Diagramm	Optische Weglänge
			$$ A \sqrt{3} $$ $$  \approx 1,7321 A $$

Pentaprismen:

Strahlablenkung um 90° Erzeugen seitenverkehrte Bilder aufgrund einer einzigen Reflexion Leichte Verschiebung des Prismas beeinflusst nicht den rechten Winkel, mit dem Licht reflektiert wird Produkte ansehen

3D-Strahlengangdiagramm	2D-Strahlengangdiagramm	Entsprechendes Tunnel-Diagramm	Optische Weglänge
			$$ A \left( 2 + \sqrt{2} \right)$$ $$ \approx 3,4142 A $$

Dachkantprismen:

Strahlablenkung um 90° Erzeugen seitenrichtiges Bild Dachfläche erzeugt zusätzliche Reflexion Produkte ansehen

3D-Strahlengangdiagramm	2D-Strahlengangdiagramm	Entsprechendes Tunnel-Diagramm	Optische Weglänge
			$$ \left( 1 + \frac{\sqrt{2}}{2} \right)A $$ $$ \approx 1,7071A $$

Doveprismen:

Werden beschichtet oder unbeschichtet verwendet Unbeschichtet: Seitenverkehrtes Bild dreht sich im doppelten Winkel bei Prismendrehung Beschichtet: Seitenrichtiges Bild wird auf sich selbst zurückreflektiert Produkte ansehen

3D-Strahlengangdiagramm	2D-Strahlengangdiagramm	Entsprechendes Tunnel-Diagramm	Optische Weglänge
			$$ \frac{2 n A}{\sqrt{2 n^2 - 1} - 1} $$
			$$ B $$

Halbe Pentaprismen:

Lenken Strahlengang um 45° ab Erzeugen seitenrichtiges Bild In Kombination mit Schmidtprismen ist Aufbau von Pechanprismen möglich Produkte ansehen

3D-Strahlengangdiagramm	2D-Strahlengangdiagramm	Entsprechendes Tunnel-Diagramm	Optische Weglänge
			$$ \frac{A}{2} \left(   2 +  \sqrt{2}  \right) $$  $$  \approx  1,7071 A  $$

Schmidtprismen:

Lenken Strahlengang um 45° ab Erzeugen seitenrichtiges Bild In Kombination mit halben Pentaprismen ist Aufbau von Pechanprismen möglich Produkte ansehen

3D-Strahlengangdiagramm	2D-Strahlengangdiagramm	Entsprechendes Tunnel-Diagramm	Optische Weglänge
			$$ A \left( 2 + \sqrt{2} \right) $$  $$  \approx 3,4142 A  $$

Pechanprismen:

Invertieren das Bild, drehen das Bild um 180° Erzeugen seitenrichtiges Bild Kombination aus Schmidtprisma und halbem Pentaprisma Produkte ansehen

3D-Strahlengangdiagramm	2D-Strahlengangdiagramm	Entsprechendes Tunnel-Diagramm	Optische Weglänge
			$$ \left( 2 + \sqrt{2} \right) \left( \frac{ A_{\tiny{\text{halbes Penta}}}}{2} + A_{\tiny{\text{Schmidt}}}\right) $$ $$ \approx 3,4142 \left(  \frac{A_{\tiny{\text{halbes Penta}}}}{2} + A_{\tiny{\text{Schmidt}}} \right) $$

Rhomboidprismen:

Lateraler Strahlversatz Lateraler Strahlversatz äquivalent zu Prismenlänge Keine Invertierung des Bildes Produkte ansehen

3D-Strahlengangdiagramm	2D-Strahlengangdiagramm	Entsprechendes Tunnel-Diagramm	Optische Weglänge
			$$ 2D $$

Literatur

1. Greivenkamp, John E. Field Guide to Geometrical Optics. SPIE Optical Engineering Press, 2004.
2. Hopkins, R. E., “Mirror and Prism Systems," in Military Standardization Handbook: Optical Design, MIL-HDBK 141, U.S. Defense Supply Agency Washington, DC, 1962.
3. Shack, Roland V. “Prisms.” In OPTI 421/521 - Introductory Optomechanical Engineering, University of Arizona, 2016.