Überblick über die Laserstrahlformung
Dies sind die Abschnitte 5.1, 5.2, 5.3, 5.4, 5.5 und 5.6 des Leitfadens für Laseroptiken.
Die Form eines Laserstrahls wird typischerweise durch seine Bestrahlungsstärkeverteilung und Phase definiert. Die Phase trägt wesentlich zur Gleichförmigkeit des Strahlprofils über die Ausbreitungsstrecke bei. Daher sind Strahlformer so konzipiert, dass sie die Bestrahlungsstärke und die Phase eines optischen Strahls umverteilen, um ein gewünschtes Strahlprofil zu erreichen, das entlang der gewünschten Ausbreitungsstrecke erhalten wird. Zu den gebräuchlichsten Bestrahlungsstärkeverteilungen gehören die Gaußverteilung, bei der die Bestrahlungsstärke mit zunehmendem radialem Abstand abnimmt, und die Flat-Top-Verteilung, auch Top-Hat genannt, bei der die Bestrahlungsstärke über einen bestimmten Bereich konstant ist (Abbildung 1). Eine detaillierte Beschreibung zur Ausbreitung von Gaußstrahlen finden Sie in unserem Anwendungshinweis Ausbreitung gaußscher Strahlen und Informationen zur Quantifizierung der Qualität der Bestrahlungsstärkeverteilung eines Lasers finden Sie in unserem Anwendungshinweis Laserresonatormoden.

Abbildung 1: Für ein gaußsches Strahlprofil (links) nimmt die Bestrahlungsstärke mit zunehmendem Abstand vom Zentrum gemäß einer gaußschen Gleichung ab. Bei einer Flat-Top-Verteilung (rechts) ist die Bestrahlungsstärke über eine bestimmte Fläche konstant.
Einige Anwendungen profitieren von Strahlprofilen, die sich vom typischen Gaußprofil einer Laserquelle unterscheiden. Beispielsweise sind Flat-Top-Profile in bestimmten Materialbearbeitungssystemen vorteilhaft, da sie oft zu genaueren und vorhersehbareren Schnitten und Kanten führen als Gaußstrahlen (Abbildung 2). Die Einführung einer strahlformenden Optik erhöht jedoch die Systemkomplexität und die Kosten.
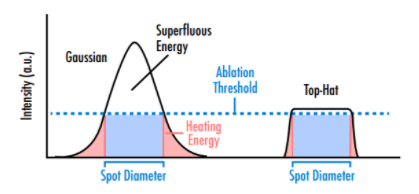
Abbildung 2: Strahlen mit Gaußprofilen sind bei Laserabtragungsanwendungen weniger effizient als solche mit Flat-Top-Profilen, da sowohl ein großer Strahlbereich mit überflüssiger Energie oberhalb der erforderlichen Abtragschwelle als auch Energie unterhalb der Schwelle in den äußeren Bereichen des Gaußprofils vorhanden ist.
Die Strahlformung modifiziert die Eigenschaften des Lichts auf ihrer grundlegendsten Ebene und ihre Effizienz wird durch die Heisenbergsche Unschärferelation zur Zeit-Bandbreite bestimmt:1
X steht für die Position und v für den Impuls. Das Unschärfeprinzip bringt einige Einschränkungen bei der Konstruktion von Strahlformern mit sich. Zum Beispiel werden bei einem Design mit sehr gut definierter Position die räumlichen Frequenzen weniger gut definiert. Wendet man die Unschärferelation auf die Beugungstheorie an, z. B. auf die Fourier-Transformationsbeziehung im Fresnel-Integral, erhält man einen charakteristischen Parameter :
ist dabei die Halbwertsbreite des Eingangsstrahls, die Halbwertsbreite des Ausgangsstrahls, eine Konstante, die Wellenlänge und der Abstand zur Ausgangsebene. Der Wert von ist sehr wichtig, wenn eine Strahlformungsanwendung entworfen oder in Erwägung gezogen wird, da größere Werte einer besseren Strahlformungsleistung entsprechen. Für beispielsweise wird der Strahlformer für praktisch jede Laseranwendung keine akzeptablen Ergebnisse liefern, während ein eine geringe Leistung liefern würde. Für eine optimale Leistung sollten daher Versuchsbedingungen verwendet werden, die zu führen. Die Formel impliziert, dass es einfacher ist, Strahlformer für größere Strahlen, kürzere Wellenlängen und kürzere Fokusabstände zu konstruieren.
Refraktive Strahlformung
In Systemen mit geringer Qualität, bei denen die Kosten ein treibender Faktor sind, werden Gaußstrahlen manchmal durch eine Blende abgeschnitten, um ein pseudo-flaches Flat-Top-Profil zu erzeugen. Dies ist ineffizient und verschwendet die Energie in den äußeren Regionen des Gaußprofils, aber es minimiert die Systemkomplexität und die Kosten.
Bei qualitativ hochwertigeren Anwendungen, die mehr Effizienz erfordern, werden häufig sowohl refraktive als auch diffraktive Laserstrahlformer eingesetzt. Diese Baugruppen verwenden typischerweise feldzuordnende Phasenelemente, wie Asphären oder Freiformlinsen und diffraktive Elemente, um die Bestrahlungsstärke und das Phasenprofil des Laserlichts umzuverteilen. Abbildung 3 zeigt das Beispiel eines refraktiven Feld-Mappers, der ein gaußsches Strahlprofil durch Wellenfrontverzerrung und die Energieerhaltungsbedingung in ein Flat-Top-Profil transformiert.2 Beim Durchgang durch die beiden Linsenelemente in einer Galilei- oder Kepler-Anordnung werden Amplitude und Phase des einfallenden Strahls geändert. Diese Art der Strahlformung ist hocheffizient (>96% Durchsatz) und innerhalb des Designbereichs wellenlängenunabhängig. Refraktive Strahlformer ermöglichen eine gleichmäßige Bestrahlungsstärkeverteilung und flache Phasenfronten.

Abbildung 3: Beispiel für refraktive Strahlformung mit Field-Mapping2
Die Fokussierung eines Flat-Top-Strahls durch eine Linse führt nicht zu einem Flat-Top-Profil beim fokussierten Punkt, da die Linse das Strahlprofil beeinflusst. Wenn ein Flat-Top-Profil beim fokussierten Punkt gewünscht ist, werden stattdessen Feld-Mapper verwendet, um einen Gaußstrahl in ein kollimiertes Airy-Scheibchen-Profil umzuwandeln, das nach der Fokussierung durch eine beugungsfreie Linse Punkte mit Flat-Top-Profil bildet (Abbildung 4).

Abbildung 4: Einige Strahlformer, wie z. B. der AdlOptica Focal-πShaper Q Flat-Top-Laserstrahlkonverter, wandeln einfallende Gaußstrahlen in Airy-Scheibchen-Profile um, sodass sie nach der Fokussieroptik zu Flat-Top-Profilen werden.
Diffraktive Strahlformung
Diffraktive Strahlformer nutzen die Beugung anstelle der Brechung, um den Laserstrahl in eine bestimmte Strahlungsverteilung zu bringen. Für die Herstellung diffraktiver Elemente wird ein Ätzprozess verwendet, um Mikro- oder Nanostrukturen in einem Substrat zu erzeugen. Typischerweise sind die Designwellenlängen und die Funktion des Elements von der Zonenhöhe bzw. dem Zonenabstand abhängig. Daher sollten diffraktive optische Elemente immer bei ihrer Designwellenlänge eingesetzt werden, um Leistungseinbußen zu vermeiden. Im Vergleich zu refraktiven Strahlformern sind diffraktive Elemente auch stärker von der Ausrichtung, der Divergenz und der Strahlposition in der Ebene des nominalen Arbeitsabstands abhängig. Andererseits sind diffraktive optische Elemente in platzbeschränkten Laseraufbauten sehr vorteilhaft, da sie in der Regel aus einem einzigen Element bestehen und nicht aus mehreren brechenden Linsen.
Laserstrahlintegratoren
Ein Laserstrahlintegrator oder Homogenisator besteht aus mehreren Mikrolinsen, die den Strahl in eine Reihe kleinerer Strahlen aufteilen, gefolgt von einer Linse oder einem anderen Fokussierelement, das die kleinen Strahlen in der Zielebene überlagert. Sie können sowohl mit kohärentem Laserlicht als auch mit anderen inkohärenten Lichtquellen verwendet werden. Typischerweise ist das endgültige Ausgangsstrahlprofil die Summe der durch das Mikrolinsen-Array erzeugten Beugungsmuster. Die meisten Laserstrahlintegratoren werden verwendet, um aus einfallenden Gaußstrahlen ein homogenisiertes Flat-Top-Profil zu erzeugen. Bei Strahlhomogenisatoren treten in der Regel zufällige Bestrahlungsstärkeschwankungen auf, was zu einem nicht perfekt ebenen Strahlprofil führt. Nicht beugungsbasierte Strahlintegratoren, wie z. B. Abbildungsintegratoren oder Wellenleiter, sind auch für räumlich inkohärentes Licht geeignet. Die Wahl zwischen Beugungs- oder Abbildungsintegrator hängt von der Fresnel-Zahl ab. Als Faustregel gilt, dass für Fresnel-Zahlen <10 ein Abbildungsintegrator benötigt wird, um ein sehr gleichmäßiges Flat-Top-Profil zu erzeugen.3
| Brechend | Diffraktiv | Strahlintegratoren | |
| Prinzip der Formung | deterministisch | deterministisch | zufällig oder quasi-zufällig |
| Zufällige Schwankungen | gering | gering | hoch |
| Ausrichtungsempfindlichkeit | gering | gering | hoch |
| Gleichmäßigkeit des Ausgangsstrahls | hoch | mittel-hoch | gering |
| Kosten | hoch | mittel | gering |
| Größe | groß | klein | klein |
Tabelle 1: In dieser Tabelle werden verschiedene Technologien für die Laserstrahlformung verglichen.
Axikons zur Erzeugung von Bessel-Strahlen
Bisher haben wir die Lichtformung mittels Feld-Mapping oder Strahlintegration besprochen, bei der Beugungseffekte eine große Rolle für das Design und die qualitative Leistung der Optik spielen. Beugung ist die Abweichung des Lichts von der geradlinigen Ausbreitung, die nicht durch Reflexion oder Brechung verursacht wird. Beugungseffekte führen dazu, dass Laserstrahlen bei ihrer Ausbreitung divergieren. Ein Strahl, dessen Profil durch eine Bessel-Funktion beschrieben wird, die als exakte und unveränderliche Lösung der Helmholtz-Gleichung definiert ist, erfährt dagegen keine Beugung, d. h. er weitet sich bei der Ausbreitung nicht auf.4 Diese Strahlen sind außerdem selbstheilend, d. h. sie können sich nach einem Hindernis an jedem beliebigen Punkt neu formen. Ideale Bessel-Strahlen sind jedoch unmöglich zu erzeugen, da sie eine unendliche Energiemenge benötigen würden. Stattdessen können durch Interferenz von ebenen Wellen, die durch eine konische Fläche wie z. B. ein Axikon gebildet werden, annähernde Bessel-Strahlen erzeugt werden, die auch als Quasi-Bessel-Strahlen bezeichnet werden.
Axikons bilden einen Quasi-Bessel-Strahl mit nahezu keiner Beugung über einen bestimmten Bereich, der als die Tiefenschärfe (DOF) bezeichnet wird. Nach diesem Bereich breitet sich der Strahl ringförmig weiter aus (Abbildung 5). Traditionelle, refraktive Axikons sind entweder konische Linsen oder Prismen. Das Licht fällt durch sie hindurch und wird an der konischen Oberfläche gebrochen. In bestimmten Situationen, wie z. B. bei Ultrakurzpuls-Lasersystemen, werden auch reflektierende Axikons mit einer reflektierenden konischen Oberfläche eingesetzt. Die breite Wellenlängenbandbreite, die Ultrakurzpulslasern eigen ist, würde bei der Übertragung durch ein brechendes Axikon eine signifikante chromatische Dispersion erfahren, während diese Dispersion bei reflektierenden Axikons vermieden wird (Abbildung 6). Quasi-Bessel-Strahlen können auch mit holographischen Methoden mit hohen Beugungseffizienzen erzeugt werden, allerdings tritt hier ein beugungsmoduliertes axiales Profil auf.

Abbildung 5: Schema eines traditionellen brechenden Axikons, das den Bessel-Strahl im DOF und den ringförmigen Strahl zeigt, der sich nach dem Überlappungsbereich ausbreitet.

Abbildung 6: Schema eines reflektierenden Axikons, das wie das traditionelle Axikon einen Bessel-Strahl im DOF und einen ringförmigen Strahl nach dem Überlappungsbereich erzeugt, aber im Gegensatz zu traditionellen Axikons unabhängig von der Wellenlänge ist.
Bessel-Strahlen erfahren wenig bis keine Beugung innerhalb ihrer Ausbreitungsstrecke und bieten eine ausgezeichnete DOF, was sie ideal für Anwendungen wie Lasermaterialbearbeitung und Hornhautchirurgie macht. Durch den gleichmäßigen Strahldurchmesser können im DOF saubere Schnitte mit scharfen Kanten erzeugt werden.
Strahlzirkularisierung mit Zylinderlinsen
Eine weitere Art der Laserstrahlformung ist das Zirkularisieren eines Strahls, bei dem ein ovales oder anders geformtes Profil in ein kreisförmiges Profil umgewandelt wird. Laserdioden ohne Kollimationsoptik haben aufgrund der rechteckigen Form des aktiven Bereichs der Diode unterschiedliche Divergenzwinkel in der x- und y-Achse, was zu länglichen Strahlformen führt (Abbildung 7). Allerdings sind oft kreisförmige Profile gewünscht, um symmetrische, kompakte Fokuspunkte zu erzeugen.
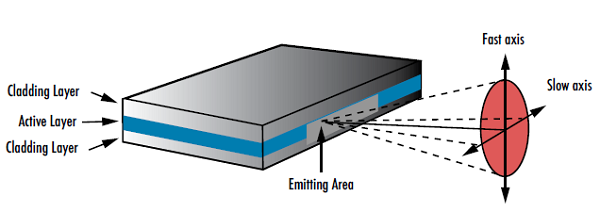
Abbildung 7: Die Geometrie von Laserdioden bewirkt, dass elliptische Strahlen mit zwei verschiedenen Divergenzwinkeln entstehen.
Wie standardmäßige sphärische Linsen verwenden Zylinderlinsen gekrümmte Oberflächen, um Licht zu konvergieren oder zu divergieren, aber sie haben nur in einer Dimension eine optische Brechkraft. Zylinderlinsen beeinflussen also das Licht nicht in der Senkrechten. Dieser Effekt kann mit normalen sphärischen Linsen nicht erreicht werden, da das Licht gleichmäßig rotationssymmetrisch fokussiert oder divergiert wird. Zylinderlinsen können somit ideal für die Formung von Laserlichtflächen und die Zirkularisierung elliptischer Strahlen eingesetzt werden.
Das Bezugssystem von Zylinderlinsen ist durch zwei orthogonale Dimensionen definiert: die Brechungsrichtung und die Nicht-Brechungsrichtung. Die "Brechungsrichtung" verläuft entlang der gekrümmten Länge der Linse und ist die einzige Achse der Linse mit optischer Brechkraft (Abbildung 8). Die "Nicht-Brechungsrichtung" der Zylinderlinse verläuft quer dazu und besitzt keine optische Brechkraft. Die Größe der Zylinderlinse entlang der Nicht-Brechungsrichtung kann variieren, ohne die optische Leistung der Linse zu beeinflussen. Zylinderlinsen können in einer Vielzahl von Geometrien hergestellt werden und haben z. B. eine rechteckige, quadratische, kreisförmige oder elliptische Form.
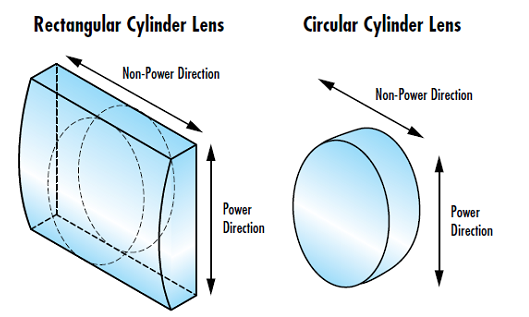
Abbildung 8: Brechungs- und Nicht-Brechungsrichtung bei rechteckigen und kreisförmigen Zylinderlinsen
Da Laserdioden asymmetrisch divergieren, kann keine sphärische Optik verwendet werden, um bei einer Diode einen kreisförmigen und kollimierten Strahl zu erzeugen. Die Sphäre wirkt auf beide Achsen gleichzeitig, wodurch die ursprüngliche Asymmetrie im Strahl erhalten bleibt. Durch ein orthogonales Zylinderlinsenpaar, kann jede Strahlachse separat geformt werden.
Das Verhältnis der Brennweiten der beiden Linsen sollte dem Verhältnis der x- und y-Strahldivergenzen entsprechen, um einen symmetrischen Ausgangsstrahl zu erhalten. Ähnlich wie bei der Standardkollimation wird die Laserdiode im gemeinsamen Brennpunkt der beiden Linsen platziert und der Abstand zwischen den Linsen sollte gleich der Differenz der beiden Brennweiten sein (Abbildung 9).
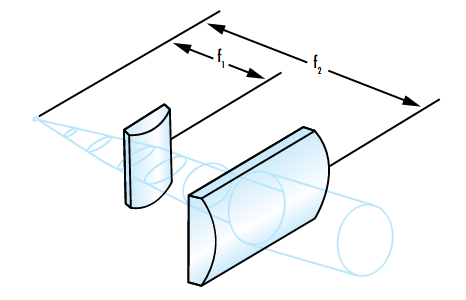
Abbildung 9: Beispiel für die Zirkularisierung eines elliptischen Strahls mit Zylinderlinsen
Die kleinen Ausgangsaperturen von Laserdioden können zu sehr großen Divergenzwinkeln führen, was bei dem Versuch, den Strahl zu kollimieren, eine Herausforderung darstellen kann. Die Divergenz hat eine direkte Auswirkung sowohl auf die zulässige Länge des Systems als auch auf die erforderlichen Größen der Linsen. Der Zusammenhang zwischen Divergenz und Strahlgröße ist in unserem Anwendungshinweis Ausbreitung gaußscher Strahlen beschrieben. Da die Positionen der einzelnen Zylinderlinsen aufgrund ihrer Brennweite relativ fest vorgegeben sind, ist es möglich, die maximale Strahlbreite an jeder Linse mit Hilfe der Brennweite der Linse und dem Divergenzwinkel der kollimierenden Linsenachse zu berechnen. Die freie Apertur jeder Linse muss dann größer sein als die entsprechende maximale Strahlbreite, um eine Beschneidung des Strahls zu vermeiden.
Weitere Informationen zu Zylinderlinsen finden Sie in unserem Anwendungshinweis Überlegungen zur Verwendung von Zylinderlinsen.
Strahlzirkularisierung mit anamorphischen Prismenpaaren
Anamorphische Prismenpaare sind eine weitere Art von Optiken, die zur Zirkularisierung elliptischer Strahlen verwendet werden können. Anamorphische Prismenpaare bestehen aus zwei Prismen, die zusammen zur Umformung eines Laserstrahls verwendet werden. Sie werden typischerweise verwendet, um elliptische Strahlprofile in kreisförmige Profile umzuwandeln, sie können aber auch andere elliptische Strahlprofile in verschiedenen Größen erzeugen. Das optische Prinzip, das hinter der Umformung steckt, ist das gleiche wie bei Zylinderlinsen: Brechung. Das Licht wird in einer Richtung bzw. einer Achse umgelenkt, während die andere Achse konstant bleibt (Abbildung 10). Dadurch werden die unterschiedlichen Divergenzwinkel des Strahls ausgeglichen.

Abbildung 10: Ein anamorphisches Prismenpaar funktioniert in einer Richtung wie ein Strahlaufweiter und erzeugt so aus einem elliptischen Strahl einen runden Strahl.
Auch ein einzelnes Prisma könnte den Strahlradius in einer Achse ändern, würde aber auch die Strahlrichtung ändern. Somit sind zwei Prismen erforderlich, um die ursprüngliche Ausbreitungsrichtung des Strahls beizubehalten und gleichzeitig seine Elliptizität zu ändern. Anamorphische Prismenpaare behalten die Parallelität zur ursprünglichen Richtung bei, verschieben aber den Strahl senkrecht dazu. Die Verwendung von anamorphischen Prismenpaaren erfordert eine präzise Winkelausrichtung für eine einwandfreie Funktion. Es ist nicht zwingend erforderlich ein Prisma im Brewster-Winkel auszurichten, aber hilfreich. Dies ist der Einfallswinkel, bei dem keine Reflexion von p-polarisiertem Licht entsteht. Auf der anderen Seite des Prismas sollte der Lichteinfall senkrecht und die Prismenfläche antireflexbeschichtet sein, um den Durchsatz zu maximieren. Die erforderliche präzise Ausrichtung der Prismen veranlasst viele Entwickler von Optiksystemen die Prismen als vorjustiertes Paar zu kaufen.
Bei einigen hochpreisigeren Laserdioden sind schon anamorphische Prismenpaare zur Strahlzirkularisierung im Laserkopf eingebaut. Bei vielen günstigeren Laserdioden ist dies hingegen nicht der Fall. Die Kosten für die Anschaffung eines separaten anamorphischen Prismenpaares und einer preiswerteren Diode ohne integriertes anamorphisches Prismenpaar können geringer sein als die einer teureren Diode.
Zylinderlinsen haben mehr Freiheitsgrade als gefasste anamorphische Prismenpaare und sind somit noch schwieriger auszurichten. Zylinderlinsen können verkippen, anamorphische Prismen sind bei der Ausrichtung der Achsen unabhängig voneinander unempfindlicher. Bei Zylinderlinsen muss weiterhin besonders die Brennweite beachtet werden, die zum Abstand vom Diodenausgang passen muss, um einen kollimierten, zirkularen Ausgangsstrahl zu erhalten. Gefasste anamorphische Prismenpaare sind hier benutzerfreundlicher. Sie sind vorausgerichtet und haben eine feste Aufweitung, sodass Sie keine Positionierung und Assemblierung wie beim Einsatz von Zylinderlinsen vornehmen müssen. Die Prismen haben nur eine einzige Achse, die ausgerichtet werden muss, da der Anwender das Prisma lediglich in den Strahlengang schiebt. Ein Ausrichtungsschritt erübrigt sich somit und es wird wertvolle Zeit gespart und eventuelle Frustration vermieden. Die physische Position der anamorphischen Prismen relativ zur Position des einfallenden Laserstrahls ist ebenfalls weniger kritisch.
Der zusätzliche Freiheitsgrad von Zylinderlinsen führt dagegen zu mehr Flexibilität, die in Forschungsanwendungen oder bei Prototypen hilfreich sein kann. Zylinderlinsen können außerdem einen höheren Durchsatz als anamorphische Prismenpaare bieten, insbesondere, wenn die Linsen AR-Beschichtungen haben. Bei Zylinderlinsen wandert das Licht durch weniger Material verglichen mit den anamorphischen Prismenpaaren und bei den Prismen geht zusätzlich p-polarisiertes Licht verloren, wenn sie unter dem Brewster-Winkel eingesetzt werden. Weitere Informationen finden Sie in unserem Anwendungshinweis Anamorphische Prismenpaare.
| Zylinderlinsen | Anamorphische Prismenpaare | |
| Strahlversatz | kein Versatz | Versatz |
| Freiheitsgrade | hoch | gering |
| Ausrichtungsempfindlichkeit | hoch | gering |
| Durchsatz | hoch | mittel |
| Kosten | gering | gering |
| Größe | klein | klein |
Tabelle 2: Vergleich von Zylinderlinsen und anamorphischen Prismenpaaren für die Strahlzirkularisierung
Literatur:
- F. M. Dickey und S. C. Holswade, Laser Beam Shaping: Theory and Techniques, Marcel Dekker, New York (2000).
- Laskin, Alexander und Vadim Laskin. "Refractive field mapping beam shaping optics: important features for a right choice." Proc. ICALEO. Vol. 2010. (2010).
- F.M. Dickey, S.C. Hoswade, D.L. Shealy, Laser Beam Shaping Applications, Taylor & Francis, ISBN 0-8247-5941 (2005).
- J. Durnin: J. Opt. Soc. Am. A 4 (1987) 651.
Weiterführende Informationen
- Why Use a Flat Top Laser Beam?
- Eine tiefer gehende Betrachtung von Axicons
- Laserstrahlformung durch Reflexion
- Einsatz von Zylinderlinsen | Edmund Optics
- Anamorphische Prismenpaare
- Laserresonator und Resonatormoden
- Aligning Mount for AdlOptica Beamshapers
- Aligning AdlOptica πShaper
- Aligning AdlOptica Focal πShaper
- Why Choose an Achromatic Cylinder Lens?
- What are Cylinder Lenses?
- Video: Einführung zum „Laser Optics Lab“













 Vorheriger Abschnitt
Vorheriger Abschnitt















weitere regionale Telefonnummern
ANGEBOTSTOOL
Geben Sie zum Starten die Produktnummer ein.
Copyright 2023 | Edmund Optics, Ltd Unit 1, Opus Avenue, Nether Poppleton, York, YO26 6BL, UK
Die Edmund Optics GmbH Deutschland fungiert als Handelsvermittler für die Edmund Optics Ltd. in Großbritannien.
Vertragspartner ist die Edmund Optics Ltd. in Großbritannien.