Grundlagen zu optischen Prismen

Was ist ein Prisma?

Herstellung | Licht und Brechung | Bilderhändigkeit/Parität | Typen | Auswahlhilfe

Prismen sind massive Glasoptiken, die zu geometrischen und optisch wirksamen Formen geschliffen und poliert werden. Der Winkel, die Position und die Anzahl der Flächen bestimmen den Typ und die Funktion. Eine der bekanntesten Anwendungen von Prismen, die von Sir Isaac Newton experimentell demonstriert wurde, besteht darin, einen weißen Lichtstrahl in seine einzelnen Farben zu zerlegen (Abbildung 1). Diese Eigenschaft wird von Refraktometern und spektrographischen Geräten genutzt. Seit dieser ersten Entdeckung wurden Prismen zum "Biegen" von Licht in einem System, zum "Falten" des Systems in einen kleineren Raum, zum Ändern der Ausrichtung eines Bildes (auch bekannt als Händigkeit oder Parität) sowie zum Kombinieren oder Aufteilen optischer Strahlen mithilfe von teilreflektierenden Oberflächen verwendet. Diese Anwendungen sind bei Teleskopen, Ferngläsern, Vermessungsgeräten und vielen anderen Geräten üblich.

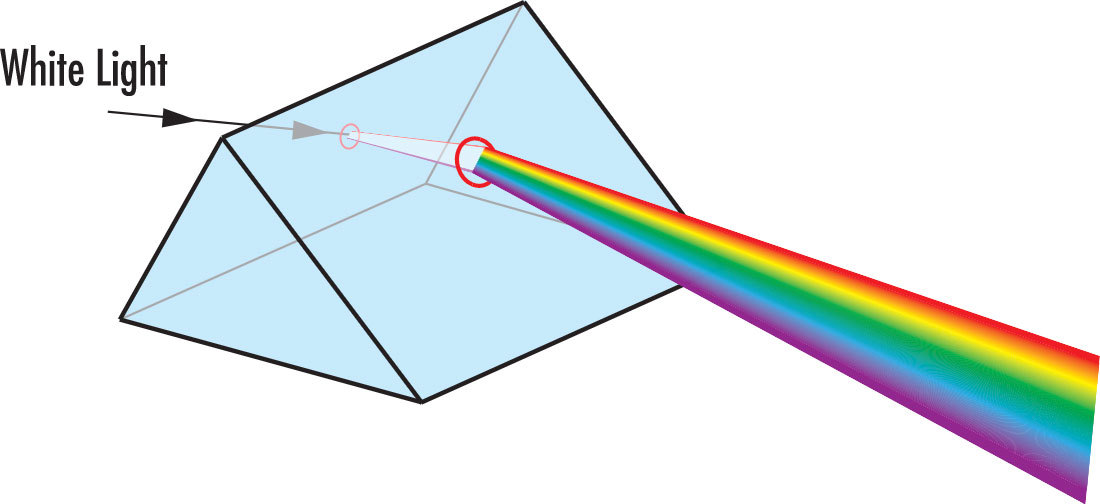
Abbildung 1: Dispersion durch ein Prisma

Bei Prismen besteht die Möglichkeit sie als ein System von ebenen Spiegeln zu modellieren, um die Reflexion von Licht innerhalb des Prismenmediums zu simulieren. Das Ersetzen von Spiegeln ist vielleicht die nützlichste Anwendung von Prismen, da sie sowohl das Licht umlenken oder falten als auch die Bildparität ändern. Oft werden mehrere Spiegel benötigt, um ähnliche Ergebnisse wie mit einem einzelnen Prisma zu erzielen. Durch die Verwendung eines Prismas anstelle mehrerer Spiegel werden mögliche Ausrichtungsfehler reduziert, die Genauigkeit erhöht und die Größe und Komplexität des Systems minimiert.

PRISMENFERTIGUNG

Bevor wir uns mit der Theorie hinter Prismen befassen, sollten wir ihren Herstellungsprozess näher betrachten. Um in Anwendungen erfolgreich eingesetzt werden zu können, müssen Prismen mit sehr engen Toleranzen und hohen Genauigkeiten gefertigt werden. Aufgrund der Variabilität von Form, Größe und vor allem der Anzahl der Oberflächen ist ein groß angelegter, automatisierter Prozess zur Herstellung von Prismen nicht realistisch. Außerdem werden die meisten Hochpräzisionsprismen nur in geringen Mengen hergestellt, sodass ein automatisiertes Verfahren unnötig wäre.

Zunächst wird ein Glasblock (ein so genannter "Rohling") einer bestimmten Glasgüte und eines bestimmten Glastyps hergestellt. Dieser Block wird dann mit einer Metalldiamantscheibe zu einem nahezu fertigen Produkt geschliffen. In dieser Phase wird ein Großteil des Glases schnell entfernt, was zu flachen, aber immer noch rauen Oberflächen führt (Abbildung 2a). Zu diesem Zeitpunkt kommen die Abmessungen des künftigen Prismas den gewünschten Spezifikationen schon sehr nahe. Anschließend folgt ein Feinschleifprozess, bei dem die unter der Oberfläche liegenden Risse entfernt werden; dieser Schritt wird als Glätten bezeichnet. Eventuelle Kratzer aus der ersten Stufe werden in der zweiten Stufe entfernt (Abbildung 2b). Nach dem Glätten sollten die Glasflächen trüb und undurchsichtig erscheinen. In den ersten beiden Phasen muss die Prismenoberfläche nass sein, um die Glasentfernung zu beschleunigen und eine Überhitzung des Glases zu vermeiden.

In der dritten Stufe wird das Prisma auf die vorgeschriebene Ebenheit poliert. In dieser Phase wird das Glas an einem Polyurethan-Polierer gerieben, der mit einem „Schlamm“ befeuchtet ist, einem Optikpoliermittel, das in der Regel aus Wasser gemischt mit Bimsstein oder Ceriumoxid besteht (Abbildung 2c). Die genaue Dauer des Poliervorgangs hängt stark von den geforderten Oberflächeneigenschaften ab. Sobald das Polieren abgeschlossen ist, kann das Anfasen beginnen. In diesem vierten Schritt werden die Kanten des Prismas mit einer sich drehenden Diamantplatte behandelt, um die scharfen Kanten, die in den vorangegangenen Schritten entstanden sind, leicht abzustumpfen (Abbildung 2d). Nach dem Anfasen wird das fertige Prisma gereinigt, geprüft (sowohl manuell als auch automatisch) und gegebenenfalls mit Antireflexions- und/oder Metallspiegelbeschichtungen versehen, um die Gesamttransmission und/oder Reflexion zu verbessern. Die Stufen Formung, Glätten, Polieren und Anfasen sind in den Abbildungen 2a - 2d grob skizziert, der reale Fertigungsprozess ist allerdings sehr viel aufwändiger und erfordert aufgrund der Anzahl der Prismenflächen mehr Iterationen oder Arbeitsgänge.

Abbildung 2a: Prisma Herstellungsprozess: Formung

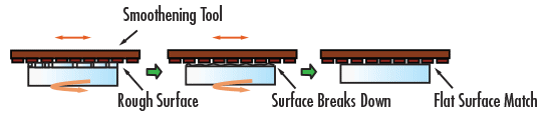
Abbildung 2b: Prisma Herstellungsprozess: Glätten

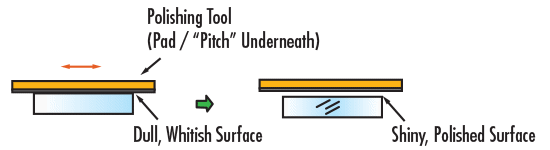
Abbildung 2c: Prisma Herstellungsprozess: Polieren

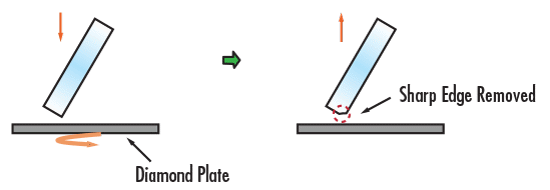
Abbildung 2d: Prisma Herstellungsprozess: Anfasen

Während der Herstellung eines Prismas muss jede zu bearbeitende Fläche kontinuierlich ausgerichtet und gesichert werden. Für die Befestigung eines Prismas gibt es zwei Methoden: Blockbefestigung und Kontaktierung. Bei der Blockbefestigung wird das Prisma in ein Metallwerkzeug mit heißem Wachs gelegt. Bei der Kontaktierung hingegen handelt es sich um ein optisches Kontaktverfahren bei Raumtemperatur, bei dem zwei saubere Glasoberflächen einfach durch ihre Van-der-Waals-Wechselwirkung miteinander verbunden werden. Die Kontaktierung wird verwendet, wenn hohe Präzisionstoleranzen erforderlich sind, da sie keine zusätzlichen Anpassungen während der Formungs-, Glättungs- oder Polierphasen erfordert, um die Wachsdicke zwischen der Prismenoberfläche und dem Block zu berücksichtigen.

In jeder Phase des Prismenherstellungsprozesses, von der Formung über die Blockbefestigung bis zur Kontaktierung, muss ein geschulter Optikspezialist die zu bearbeitenden Prismenoberflächen manuell überprüfen und anpassen. Aus diesem Grund ist die Fertigung äußerst arbeitsintensiv, Erfahrung und Geschick sind zwingende Voraussetzungen. Der gesamte Prozess erfordert viel Zeit, Arbeit und Konzentration.

THEORIE: LICHT UND BRECHUNG

Das Verständnis der Funktionsweise eines Prismas ist der Schlüssel zur Entscheidung, welche Art von Prisma am besten für eine bestimmte Anwendung geeignet ist. Dazu ist es zunächst wichtig zu verstehen, wie Licht mit einer optischen Oberfläche interagiert. Diese Wechselwirkung wird durch das Snelliussche Brechungsgesetz beschrieben:

Dabei ist $ \small{n_1} $ der Index des einfallenden Mediums, $ \small{\theta_1} $ ist der Winkel des einfallenden Strahls, $ \small{n_2} $ ist der Index des brechenden/reflektierenden Mediums und $ \small{\theta_2} $ ist der Winkel des gebrochenen/reflektierten Strahls. Das Snelliussche Brechungsgesetz beschreibt die Beziehung zwischen den Einfalls- und Transmissionswinkeln, wenn sich ein Strahl von einem in ein anderes Medium bewegt (Abbildung 3).

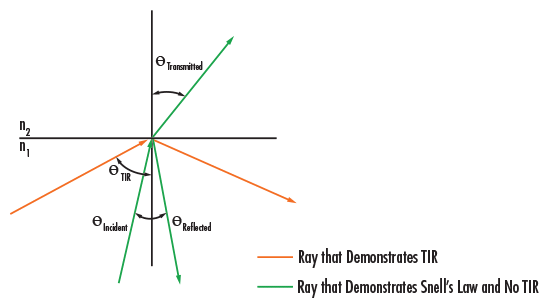
Abbildung 3: Snelliussches Gesetz und interne Totalreflexion

Ein Prisma zeichnet sich dadurch aus, dass es den Strahlengang reflektieren kann, ohne dass eine besondere Beschichtung erforderlich ist, wie sie bei der Verwendung eines Spiegels benötigt wird. Dies wird durch ein Phänomen erreicht, das als interne Totalreflexion (TIR) bekannt ist. TIR tritt auf, wenn der Einfallswinkel (Winkel des einfallenden Strahls gemessen von der Normalen) größer ist als der kritische Winkel $ \small{\theta_c} $:

Dabei ist $ \small{n_1} $ der Brechungsindex des Mediums, in dem der Strahl beginnt, und $ \small{n_2} $ der Brechungsindex des Mediums, aus dem der Strahl austritt. Es ist wichtig zu wissen, dass TIR nur dann auftritt, wenn das Licht von einem Medium mit hohem Brechungsindex zu einem Medium mit niedrigem Brechungsindex wandert.

Im kritischen Winkel ist der Brechungswinkel gleich 90°. In Abbildung 3 ist zu sehen, dass TIR nur dann auftritt, wenn $ \small{\theta} $ den kritischen Winkel überschreitet. Liegt der Winkel unterhalb des kritischen Winkels, so kommt es gemäß dem Snelliusschen Brechungsgesetz neben der Reflexion auch zur Transmission. Entspricht eine Prismenfläche nicht den TIR-Spezifikationen für den/die gewünschten Winkel, muss eine reflektierende Beschichtung verwendet werden. Aus diesem Grund erfordern manche Anwendungen beschichtete Versionen eines Prismas, das in einer anderen Anwendung auch unbeschichtet gut funktionieren würde.

THEORIE: BILDHÄNDIGKEIT/PARITÄT

Ein wichtiger Aspekt bei der Abbildung durch ein Prisma ist die Händigkeit (Parität) des Bildes, die auch als Bildausrichtung bezeichnet wird. Die Bildausrichtung wird jedes Mal geändert, wenn der Strahlengang auf einen ebenen Spiegel, eine flache reflektierende Oberfläche oder eine Prismenoberfläche in einem Winkel trifft, der TIR erzeugt. Es gibt zwei Arten von Händigkeit: rechts und links. Rechtshändigkeit (Abbildung 4) beschreibt den Fall, in dem ein Bild einer geraden Anzahl von Reflexionen unterliegt, sodass es (unter der Annahme, dass es sich bei dem Bild um Text handelt) in mindestens einer Position deutlich gelesen werden kann. Die Linkshändigkeit (Abbildung 5) beschreibt den Fall, dass das Bild eine ungerade Anzahl von Reflexionen erfährt, was zu einer Veränderung des Bildes führt, die mit der eines Spiegels vergleichbar ist.

Abbildung 4: Rechtshändigkeit oder gerade Parität

Abbildung 5: Linkshändigkeit oder ungerade Parität

Neben der Parität gibt es drei Arten der Bildänderung (Abbildung 6). Eine Inversion ist eine Spiegelung an einer horizontalen Achse, während eine Reversion eine Spiegelung an einer vertikalen Achse ist. Wenn beides gleichzeitig geschieht, wird das Bild um 180° gedreht, ohne dass sich die Parität ändert. Man kann die Parität auch erklären, indem man sich vorstellt, dass der Blick entgegen der Ausbreitungsrichtung auf das Objekt oder das Bild in seinem optischen Raum gerichtet ist (Abbildung 7).

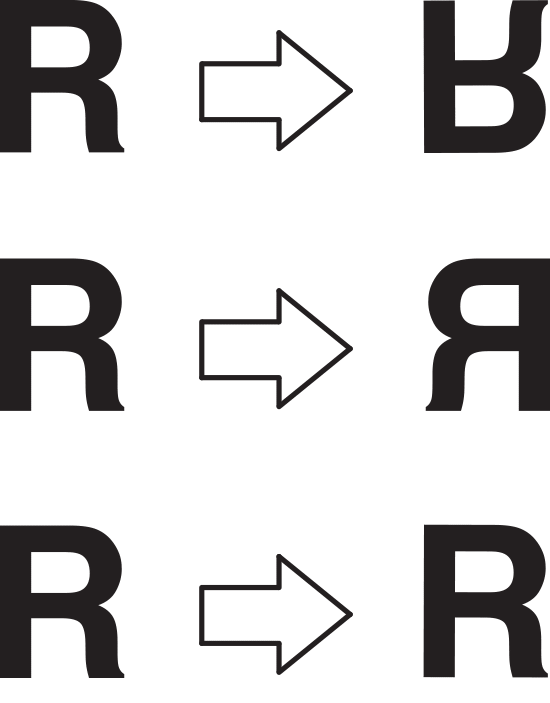
Abbildung 6: Inversion (oben), Reversion (Mitte) und Drehung (unten)

Abbildung 7: Wie die Parität bestimmt wird

Bei der Verwendung eines Prismas sollten Sie die folgenden vier Punkte beachten:

1. Die Händigkeit des Bildes ändert sich jedes Mal, wenn ein Bild reflektiert wird.
2. Jeder Punkt auf der Ebene der spiegelnden Oberfläche ist gleich weit vom Objekt und seinem Bild entfernt.
3. Das Snelliussche Brechungsgesetz kann auf alle Oberflächen angewendet werden.
4. Beim Testen der Händigkeit/Parität des Bildes ist es am besten, einen nicht-symmetrischen Buchstaben wie R, F oder Q zu verwenden. Vermeiden Sie Buchstaben wie X, O, A, usw.

WAS IST DIE PYRAMIDALTOLERANZ?

Einige Prismen, wie z. B. rechtwinklige Prismen und Dachkantprismen, haben häufig eine spezifizierte Pyramidaltoleranz oder einen zulässigen Pyramidalfehler. Dabei handelt es sich nicht um einen der physikalischen Winkel des Prismas, sondern vielmehr um eine Methode zur Beschreibung der Genauigkeit der Flächen des Prismas in Bezug aufeinander. Wenn alle Flächen in einem perfekten Prisma ausgedehnt würden, würde die gleiche Form für immer bestehen bleiben. Dies wäre ein Pyramidalfehler von Null. In der Realität wird es bei Prismenflächen einen kleinen Ausrichtungsfehler geben, der bei Ausdehung der Prismenflächen schließlich zu einer Pyramidenform führen würde. Der Winkel an der Spitze dieser theoretischen Pyramide ist der Pyramidalfehler. Er wird aus der Projektion einer Kante des Prismas auf die Linie berechnet, die zwischen den Kanten auf der gegenüberliegenden Seite des Prismas verläuft.

Typische Pyramidaltoleranzen für Präzisionsprismen liegen zwischen 1-3 Bogenminuten. Kommerzielle Qualitätsprismen haben oft Toleranzen im Bereich von 5-10 Bogenminuten. Die Pyramidaltoleranz ist im Wesentlichen eine Neigungstoleranz auf den Flächen, die senkrecht zu den Dreiecken eines dreieckigen Prismas stehen. Normalerweise wird die Art und Weise, wie Prismen das Licht umlenken, in einer 2-dimensionalen Ebene (X-Z) betrachtet. Die Neigung aus einer Pyramidaltoleranz steht in der Y-Ebene senkrecht dazu. Bei vielen Systemen hat der Pyramidalfehler nur geringe bis gar keine Auswirkungen auf die Leistung und kann durch Neigung des Prismas ausgeglichen werden. Die Angabe kann jedoch bei einigen Anwendungen wichtig sein, bei denen die Neigung in Y nicht mechanisch verändert werden kann, um den Fehler auszugleichen. Für diese Anwendungen sind möglichst enge Pyramidaltoleranzen wichtig. Besonders bei Dachprismen kann dies herausfordernd sein.

ARTEN VON PRISMEN

Es gibt vier Haupttypen von Prismen: Dispersionsprismen, Reflexionsprismen, Prismen zur Bilddrehung (Rotationsprismen) und Verschiebeprismen. Reflexions-, Verschiebe- und Rotationsprismen werden häufig für bildgebende Anwendungen eingesetzt; Dispersionsprismen sind ausschließlich für die Streuung von Licht gedacht und daher nicht für Anwendungen geeignet, die eine hohe Bildqualität erfordern.

Dispersionsprismen

Die Prismendispersion hängt von der Geometrie des Prismas und seiner Index-Dispersionskurve ab, die auf der Wellenlänge und dem Brechungsindex des Prismensubstrats beruht. Der Winkel der minimalen Abweichung gibt den kleinsten Winkel zwischen dem einfallenden Strahl und den transmittierten Strahlen an (Abbildung 8). Die grüne Wellenlänge des Lichts wird stärker abgelenkt als die rote, und die blaue stärker als die rote und die grüne. Rot wird allgemein als 656,3 nm, Grün als 587,6 nm und Blau als 486,1 nm definiert.

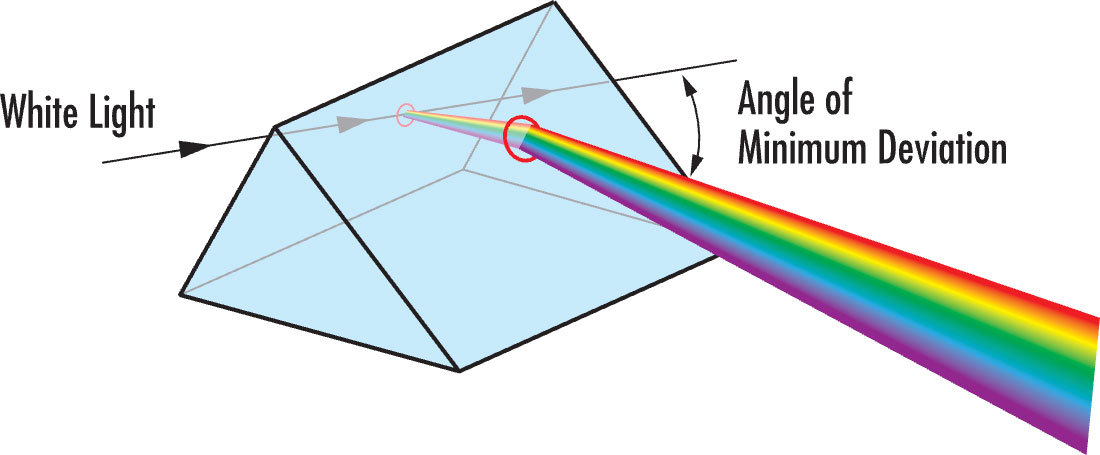
Abbildung 8: Dispersion durch ein Prisma

Reflexionsprismen

Prismen, die den Strahlengang ablenken, das Bild drehen oder einfach das Bild aus seiner ursprünglichen Achse verschieben, sind in vielen Abbildungssystemen hilfreich. Strahlen werden in der Regel in Winkeln von 45°, 60°, 90° und 180° abgelenkt. Auf diese Weise lässt sich die Systemgröße verringern oder der Strahlengang anpassen, ohne dass der Rest des Systems beeinträchtigt wird.

Prismen zur Bilddrehung (Rotationsprismen)

Rotationsprismen, wie z. B. Doveprismen, werden verwendet, um ein Bild zu drehen, nachdem es invertiert wurde.

Verschiebeprismen

Verschiebeprismen behalten die Richtung des Strahlengangs bei, passen aber sein Verhältnis zur Normalen an.

Auswahlhilfe Prismen

Um die Auswahl der besten Prismen für bestimmte Anwendungen zu erleichtern, finden Sie im Folgenden eine Auswahl der in Optik-, Bildverarbeitungs- und Photonikanwendungen am häufigsten verwendeten Prismen.

Auswahlhilfe Prismen

Equilaterale Prismen - Dispersion

Funktion Aufteilung von weißem Licht in seine Farbbestandteile Anwendung Spektroskopie Telekommunikation Wellenlängen-Trennung Mehr erfahren

Littrowprismen - Dispersion, Ablenkung

Funktion Unbeschichtet: Aufteilung von weißem Licht in seine Farbbestandteile Beschichtet: Lenken Strahlengang um 60° ab Bild ist rechtshändig Anwendung Spektroskopie (unbeschichtet) Multispektrale Laser-Systemabstimmung (beschichtet) Mehr erfahren

Rechtwinklige Prismen - Ablenkung, Verschiebung

Funktion Lenken Strahlengang um 90° ab Bild ist linkshändig Können kombiniert werden, um Bild-/Strahlversatz zu erzeugen Anwendung Endoskopie Mikroskopie Laserausrichtung Medizinische Geräte Mehr erfahren

Pentaprismen - Ablenkung

Funktion Lenken Strahlengang um 90° ab Bild ist rechtshändig Anwendung Visuelles Targeting Projektion Messung Displaysysteme Mehr erfahren

Halbe Pentaprismen - Ablenkung

Funktion Lenken Strahlengang um 45° ab Bild ist rechtshändig Anwendung Pechan-Aufrichtungsbaugruppen Mehr erfahren

Dachkantprismen - Ablenkung

Funktion Lenken Strahlengang um 90° ab Bild ist rechtshändig Anwendung Mikroskope Teleskopokulare Mehr erfahren

Schmidtprismen - Ablenkung

Funktion Lenken Strahlengang um 45° ab Bild ist rechtshändig Anwendung Stereomikroskope Pechan-Aufrichtungsbaugruppen Mehr erfahren

Retroreflektoren (Dreiflächenprismen) - Ablenkung, Verschiebung

Funktion Lenken Strahlengang um 180° ab Bild ist linkshändig Reflektiert jeden Strahl, der in die Prismenfläche eintritt, unabhängig von der Ausrichtung des Prismas, auf sich selbst zurück Anwendung Interferometrie Endoskopie Entfernungsmessung Laser-Tracking Präzise Ausrichtung Mehr erfahren

Keilprismen - Ablenkung, Drehung

Funktion Einzeln verwendet, um einen Laserstrahl um einen bestimmten Winkel abzulenken Kombination aus zwei Prismen, um ein anamorphes Paar für die Strahlformung zu erstellen Anwendung Strahllenkung Durchstimmbare Laser Anamorphische Bildgebung Forstwirtschaft Mehr erfahren

Rhomboidprismen - Verschiebung

Funktion Verschieben die optische Achse ohne Änderung der Händigkeit Richtung bleibt gleich (keine Strahlenablenkung) Anwendung Ferngläser Entfernungsmesser Lasergeräte Mehr erfahren

Doveprismen - Drehung

Funktion Unbeschichtet: Drehen ein Bild um das Doppelte des Prismenwinkels Unbeschichtet: Bild ist linkshändig Beschichtet: Reflektiert jeden Strahl, der in die Prismenfläche eintritt, auf sich selbst zurück Beschichtet: Bild ist rechtshändig Anwendung Interferometrie Astronomie Erkennung von Mustern Bildgebung hinter Detektoren oder um Ecken Mehr erfahren

Anamorphische Prismenpaare - Aufweitung

Funktion Durchmesser des einfallenden Strahls in einer Dimension erweitern Ideal, um elliptische Strahlen kreisförmig zu machen Anwendung Strahlaufweiter für Laserdioden HD-Bildverarbeitungsobjektive Mehr erfahren

Homogenisierende Lichtleiterstäbe - Homogenisierung

Funktion Homogenisieren ungleichförmige Lichtquellen Anwendung LED-Beleuchtung Mikro-Projektoren Speckle-Abschwächer OEM-Beleuchtung Mehr erfahren

Spitz zulaufende homogenisierende Lichtleiterstäbe - Homogenisierung

Funktion Homogenisierung ungleichmäßiger Lichtquellen bei gleichzeitiger Verringerung der numerischen Ausgangsapertur (NA) Anwendung Projektoren Mikro-Display-Relais-Systeme Mehr erfahren

Diese Einführung hat einen Einblick in den Herstellungsprozess und die Theorie der Prismen gegeben sowie eine Auswahlhilfe geboten, die Ihnen hilft, das beste Prisma für Ihre Anwendung zu finden. Einige weitere Beispiele zum Einsatz von Prismen finden Sie unter Anwendungsbeispiele für optische Prismen.