MTF-Kurven und Abbildungsleistung
Dies ist der Abschnitt 2.6 des Leitfadens zur Bildverarbeitung.
Abbildung 1 ist ein Beispiel für eine MTF-Kurve (Modulationstransferfunktion) für ein Objektiv mit 12 mm Brennweite, das mit dem IMX250-Sensor von Sony (2/3“ und 3,45 µm Pixelgröße) eingesetzt wird. Weitere Informationen zu Sensorformaten finden Sie im Abschnitt Sensoren. Die MTF-Kurve zeigt den Objektivkontrast über einen Frequenzbereich von 0 bis 150$ \small{\tfrac{\text{lp}}{\text{mm}}} $ (die Grenz-/Nyquistauflösung des Sensors beträgt 145$ \small{\tfrac{\text{lp}}{\text{mm}}} ) $. Außerdem ist das Objektiv auf eine Blendenzahl von 2,8 und auf eine Vergrößerung von 0,05X eingestellt. Das Bildfeld (FOV), ca. 170 mm, ist etwa 20-mal so groß wie die horizontale Sensorgröße. Dieses Bildfeld und diese Vergrößerung werden für alle Beispiele in diesem Abschnitt verwendet. Die Lichtquelle wird als weißes Licht simuliert.
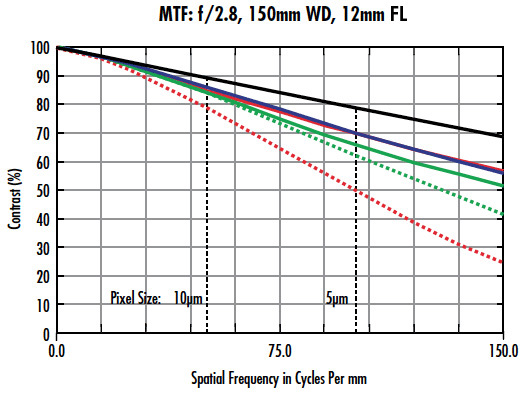
Abbildung 1: MTF-Kurve für ein Objektiv mit 12 mm Brennweite, das mit einem IMX250-Sensor von Sony eingesetzt wird.
Die obige Kurve liefert eine Vielzahl von Informationen. Zunächst ist zu beachten, dass die schwarze Linie die Beugungsgrenze darstellt. Der maximal theoretisch erreichbare Kontrast bei der Frequenz 150 sind fast 70% und keine Änderung am Objektivdesign kann diese Leistung des Objektivs weiter erhöhen (unter der Annahme gleichbleibender Blendenzahl und Wellenlänge). Wichtig sind auch die blauen, grünen und roten Linien, die die Leistung dieses Objektivs auf dem Sensor darstellen (im Abschnitt Die Modulationsübertragungsfunktion ist erklärt welche Feldpositionen den einzelnen Farben entsprechen). Es zeigt sich deutlich, dass die Kontrastwiedergabe bei niedrigeren und höheren Frequenzen nicht über den gesamten Sensor, also nicht über das gesamte Bildfeld, gleich ist.
Vergleich von Objektivdesigns und -einstellungen
Bsp. 1: Vergleich von zwei Objektivdesigns mit gleicher Brennweite und f/#
In Abbildung 2 werden zwei verschiedene Objektive mit der gleichen Brennweite (12 mm) und Blende (f/2,8) sowie dem gleichen Sensor und dem gleichen Bildfeld verglichen. Die Bildverarbeitungssysteme mit diesen Objektiven haben die gleiche Größe, unterscheiden sich aber hinsichtlich der Leistung. Die horizontale hellblaue Linie bei 30% Kontrast zeigt in Abbildung 2a, dass mindestens 30% Kontrast fast über das gesamte Bildfeld erreicht werden, was bedeutet, dass der Sensor voll ausgenutzt wird. Bei Abbildung 2b liegt nahezu das gesamte Feld unter 30% Kontrast. Eine gute Bildqualität wird hier nur über einen kleinen Teil des Sensors erreicht. Der orangefarbene Kasten zeigt für das Objektiv mit geringerer Leistung aus Abbildung 2b die Frequenz bei 70% Kontrast an. Wenn dieselbe Box in Abbildung 2a platziert wird, ist ein enormer Leistungsunterschied zwischen den beiden Objektiven ersichtlich, selbst bei niedrigeren Frequenzen. Der Grund für den Unterschied zwischen diesen Objektiven sind die Kosten, die mit beiden Designs und Fertigungsvarianten verbunden sind. Das Objektiv aus Abbildung 2a hat ein komplexeres Design und engere Fertigungstoleranzen. Es eignet sich sowohl für Anwendungen mit geringerer als auch mit höherer Auflösung, bei denen relativ kurze Arbeitsabstände (WD) für größere Bildfelder erforderlich sind. Das Objektiv aus Abbildung 2b eignet sich am besten, wenn mehr Pixel benötigt werden, um die Wiedergabetreue von Bildverarbeitungsalgorithmen zu verbessern, und wenn geringere Kosten erforderlich sind. Beide Objektive haben funktionierende Designs für bestimmte Situationen, es kommt auf die Anwendung an. Nur weil ein Objektiv auf einem Sensor die Auflösung der Nyquistgrenze nicht erreicht, schließt dies seine Verwendung auf diesem Sensor nicht aus.


Abbildung 2: MTF-Kurven für zwei verschiedene Objektivdesigns (a und b) mit der gleichen Brennweite, f/# sowie dem gleichen Sensor und unter Verwendung der gleichen Systemparameter
Bsp. 2: Vergleich von zwei hochauflösenden Objektivdesigns mit gleicher f/#, aber unterschiedlichen Brennweiten
In Abbildung 3 werden zwei verschiedene hochauflösende Objektive mit Brennweiten von 12 mm und 16 mm und demselben Bildfeld, Sensor und derselben f/# untersucht. Betrachtet man den Kontrast des Objektivs an der Nyquistgrenze in Abbildung 3b (die hellblaue Linie), so ist eine deutliche Leistungssteigerung zu erkennen im Vergleich zu Abbildung 3a. Während der absolute Unterschied nur etwa 25% Kontrast beträgt, liegt der relative Unterschied eher bei 85%, wenn man den Wechsel von etwa 25% Kontrast auf 46% berücksichtigt. Der orangefarbene Kasten ist dort platziert, wo Abbildung 3a einen Kontrast von 70% erreicht. Beachten Sie, dass der Unterschied in der Leistung in diesem Beispiel nicht so extrem ist wie im vorherigen. Der Arbeitsabstand für das Objektiv in Abbildung 3b nimmt um etwa 33% zu, die Leistung steigt allerdings nur gering an. Dieses Phänomen stimmt mit den Punkten überein, die in Bewährte Praktiken für bessere Bildgebung beschrieben sind.


Abbildung 3: Zwei verschiedene hochauflösende Objektivdesigns mit unterschiedlichen Brennweiten bei gleicher f/# und gleichen Systemparametern
Bsp. 3: Vergleich verschiedener Blendenwerte bei demselben Objektivdesign mit 35 mm Brennweite
Abbildung 4 zeigt die MTF für ein 35-mm-Objektivdesign bei weißem Licht und mit f/4 (a) und f/2 (b). Die gelbe Linie in beiden Diagrammen zeigt den Kontrast an der Nyquistgrenze für Abbildung 4a, während die blaue Linie die niedrigste tatsächliche Leistung an der Nyquistgrenze desselben Objektivs bei f/4 in Abbildung 4a kennzeichnet. Während die theoretische Grenze von Abbildung 4b weit höher liegt, ist die tatsächliche Leistung deutlich geringer. Dieses Beispiel zeigt, dass höhere Blendenzahlen die Aberrationseffekte reduzieren können, was die Leistung des Objektivs erheblich steigert, auch wenn die theoretische Leistungsgrenze stark reduziert ist. Ein großer Nachteil der Abblendung (Erhöhung der Blendenzahl) ist allerdings neben der Auflösung der geringere Lichtdurchsatz.


Abbildung 4: MTF-Kurven für ein Objektiv mit 35 mm Brennweite bei gleichem Arbeitsabstand und verschiedenen Blendenwerten: f/4 (a) und f/2 (b)
Bsp. 4: Die Auswirkung einer Änderung des Arbeitsabstandes auf die MTF
In Abbildung 5 werden Arbeitsabstände von 200 mm (a) und 450 mm (b) für das gleiche Objektivdesign mit 35 mm Brennweite bei f/2 untersucht. Der große Leistungsunterschied hängt direkt damit zusammen, wie gut die Menge an Aberrationen in einem Objektivdesign über einen Bereich von Arbeitsabständen ausgeglichen worden ist. Eine Änderung des Arbeitsabstands, selbst bei Nachfokussierung, führt zu Abweichungen oder Leistungseinbußen, da sich das Objektiv von seinem vorgesehenen Bereich entfernt. Diese Effekte sind bei niedrigeren Blendenzahlen am stärksten ausgeprägt.
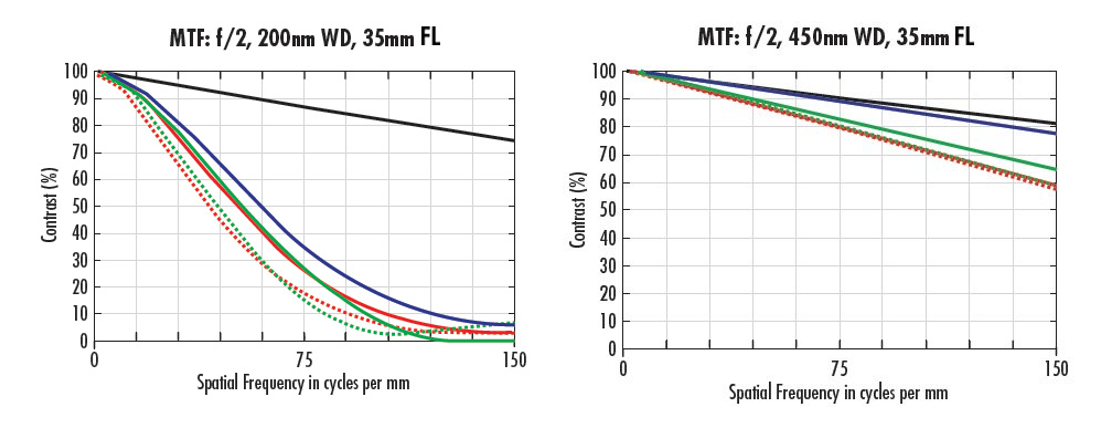
Abbildung 5: MTF-Kurven für ein Objektiv mit 35 mm Brennweite bei f/2 mit verschiedenen Arbeitsabständen
Auswirkungen der Wellenlänge auf die Leistung
Verschiedene Wellenlängen werden beim Durchgang von Licht durch ein Medium (Glas, Wasser, Luft usw.) in unterschiedlichen Winkeln abgelenkt. Dies ist zu sehen, wenn Sonnenlicht durch ein Prisma fällt und einen Regenbogeneffekt erzeugt; kürzere Wellenlängen werden stärker abgelenkt als längere. Derselbe Effekt erschwert die Auflösung und Informationsgewinnung in bildgebenden Systemen. Um dieses Problem zu vermeiden, werden in Bildgebungssystemen in der industriellen Bildverarbeitung oft monochromatische (einzelne Wellenlängen) oder schmalbandige Beleuchtungen eingesetzt. Eine monochromatische Beleuchtung (z. B. eine LED mit 660 nm) eliminiert praktisch chromatische Aberrationen in einem Abbildungssystem.
Chromatische Aberrationen
Chromatische Aberrationen existieren in zwei Formen: laterale Farbverschiebung (Abbildung 6) und chromatische Fokusverschiebung (Abbildung 7).
Die laterale Farbverschiebung, Abbildung 6, wird am Rand des Bildes besonders deutlich sichtbar. In der Mitte sind die Punkte für verschiedene Wellenlängen des Lichts konzentrisch angeordnet. In Richtung der Bildecke trennen sich die Wellenlängen und erzeugen einen Regenbogeneffekt. Aufgrund der Farbseparation wird ein bestimmter Punkt auf dem Objekt über einen größeren Bereich abgebildet, was zu einem reduzierten Kontrast führt. Bei Sensoren mit kleineren Pixeln ist dieses Ergebnis noch ausgeprägter, da sich die Unschärfe auf mehr Pixel verteilt. Details zur lateralen Farbverschiebung finden Sie im Abschnitt Aberrationen.

Abbildung 6: Darstellung eines Punktes mit lateraler Farbverschiebung
Die chromatische Fokusverschiebung, Abbildung 7, bezieht sich auf die Fähigkeit eines Objektivs, alle Wellenlängen im gleichen Abstand vom Objektiv zu fokussieren. Unterschiedliche Wellenlängen haben unterschiedliche Ebenen des besten Fokus. Diese Verschiebung des Fokus in Bezug auf die Wellenlänge führt zu einem reduzierten Kontrast, da die verschiedenen Wellenlängen unterschiedliche Punktgrößen in der Bildebene erzeugen, in der sich der Kamerasensor befindet. In der Bildebene (Image Plane) von Abbildung 7 ist eine kleine Punktgröße bei den roten Wellenlängen, eine größere Punktgröße bei grün und die größte Punktgröße bei blau dargestellt. Es können nicht alle Farben gleichzeitig fokussiert werden. Weiterführende Details finden Sie im Abschnitt Aberrationen.

Abbildung 7: Darstellung eines Punktes mit chromatischer Fokusverschiebung
Auswahl der optimalen Wellenlänge
Die monochromatische Beleuchtung erhöht den Kontrast, indem sie sowohl die chromatische Fokusverschiebung als auch die laterale chromatische Aberration eliminiert. Daher sollte immer der Einsatz von LED-Beleuchtung, Lasern oder Filtern in Betracht gezogen werden. Allerdings können verschiedene Wellenlängen unterschiedliche MTF-Effekte in einem System haben. Die Beugungsgrenze definiert den kleinsten theoretischen Punkt, der von einem perfekten Objektiv erzeugt werden kann, vorgegeben durch den Durchmesser des Airy-Scheibchens in Abhängigkeit von der Wellenlänge (λ). Mithilfe von Gleichung 1 kann die Änderung der Punktgröße sowohl für verschiedene Wellenlängen als auch für verschiedene Blendenzahlen berechnet werden.
Tabelle 1 zeigt den berechneten Airy-Scheibchendurchmesser für Wellenlängen von violett (405 nm) bis nahinfrarot (880 nm) bei verschiedenen Blendenzahlen. Diese Daten zeigen, dass Abbildungssysteme eine bessere theoretische Auflösung und qualitative Leistung haben, wenn sie mit kürzeren Wellenlängen verwendet werden. Kürzere Wellenlängen ermöglichen eine bessere Ausnutzung der Pixel des Sensors unabhängig von der Größe, da eine kleinere Punktgröße erreicht werden kann. Dies wird besonders deutlich bei Sensoren mit sehr kleinen Pixeln. Die Verwendung höherer Blendenzahlen erzeugt eine größere Tiefenschärfe. Eine rote LED kann bei f/2,8 eine Punktgröße von 4,51 µm erzeugen oder eine blaue LED kann bei f/4 fast die gleiche Punktgröße erzeugen. Wenn beide Optionen eine akzeptable Leistung bei bester Schärfe erbringen, wird das auf f/4 eingestellte System mit blauem Licht eine bessere Tiefenschärfe erzeugen, was für einige Anwendungen nützlich sein könnte.
| Farbe | Wellenlänge | Blende (f/#) | ||||
|---|---|---|---|---|---|---|
| f/1,4 | f/2,8 | f/4 | f/8 | f/16 | ||
| NIR | 880 | 3,01 | 6,01 | 8,59 | 17,18 | 34,36 |
| Rot | 660 | 2,25 | 4,51 | 6,44 | 12,88 | 25,77 |
| Grün | 520 | 1,78 | 3,55 | 5,08 | 10,15 | 20,30 |
| Blau | 470 | 1,61 | 3,21 | 4,59 | 9,17 | 18,35 |
| Violett | 405 | 1,38 | 2,77 | 3,95 | 7,91 | 15,81 |
Tabelle 1: Theoretischer Airy-Scheibchendurchmesser für verschiedene Wellenlängen und Blendenzahlen
Bsp. 5: Verbesserung durch richtige Wellenlängenwahl
Beide Bilder in Abbildung 8 wurden mit den gleichen Objektiven und der gleichen Kamera aufgenommen und erzeugen so das gleiche Bildfeld und somit auch die gleiche räumliche Auflösung auf dem Objekt. Die Kamera verwendet einen Sensor mit 3,45 µm Pixelgröße. Die Beleuchtung in Abbildung 8a hat eine Wellenlänge von 660 nm und in 8b von 470 nm. Das hochauflösende Objektiv wurde auf eine höhere Blendenzahl eingestellt, um eventuelle Aberrationseffekte stark zu reduzieren. Dadurch ist in diesem Fall die Beugung die primäre Begrenzung im System. Die blauen Kreise zeigen die Auflösungsgrenze in Abbildung 8a. Beachten Sie, dass Abbildung 8b einen deutlichen Anstieg der auflösbaren Details aufweist (ca. 50% feinere Details). Selbst bei den niedrigeren Frequenzen (breitere Linien) ist bei der Beleuchtung mit 470 nm in Abbildung 8b ein höherer Kontrast vorhanden.


Abbildung 8: Bilder des Siemenssterns, aufgenommen mit demselben Objektiv, bei derselben Blende und mit demselben Sensor. Die Wellenlänge wird von 660 nm (a) auf 470 nm (b) geändert.
Bsp. 6: MTF mit weißem Licht vs. monochromatischem Licht
In Abbildung 9 wird das gleiche Objektiv mit dem gleichen Arbeitsabstand und der gleichen Blendenzahl verwendet. Abbildung 9a zeigt eine Kurve bei weißem Licht und Abbildung 9b zeigt eine Kurve mit einer Beleuchtung bei 470 nm. In Abbildung 9a liegt die Leistung an der Nyquistgrenze (für eine Pixelgröße von 3,45 μm) bei ca. 50% oder darunter. Bei Abbildung 9b ist die Leistung an der Nyquistgrenze höher als bei Abbildung 9a. Außerdem liegt die Leistung in der Bildmitte in Abbildung 9b oberhalb der Beugungsgrenze von Abbildung 9a. Der Grund für diese Leistungssteigerung ist zweierlei: Erstens werden durch die Verwendung von monochromatischem Licht chromatische Aberrationen eliminiert, wodurch kleinere Punkte erzeugt werden können. Zweitens ist die Wellenlänge 470 nm eine der kürzesten Lichtwellenlängen, die im sichtbaren Bereich für die Bildgebung verwendet werden. Wie in den Abschnitten über Beugungsgrenze und Airy-Scheibchen beschrieben, ermöglichen kürzere Wellenlängen eine höhere Auflösung.


Abbildung 9: MTF-Kurven für dasselbe Objektiv bei f/2 unter Verwendung verschiedener Wellenlängen; weißes Licht (a) und 470 nm (b).
Überlegungen zur Wellenlänge
Beim Wechsel der Wellenlänge können einige Probleme auftreten. Objektive bekommen Probleme, wenn die Wellenlänge der Beleuchtung in die UV-Richtung tendiert (also die Wellenlänge abnimmt), unabhängig davon, ob das Wellenband schmal oder breit ist: Glasmaterialien neigen dazu, bei kürzeren Wellenlängen (niedriger als etwa 425 nm) nicht mehr so gut zu funktionieren. Es gibt zwar Designs in diesem Bereich des Spektrums, aber sie sind oft in ihren Fähigkeiten begrenzt und die seltenen Materialien, die verwendet werden, machen den Bau des Objektivs teurer. Die beste theoretische Leistung, die in Tabelle 1 zu sehen ist, liegt bei der violetten Wellenlänge 405 nm, aber die meisten realen Objektivdesigns können in diesem Bereich keine gute Leistung mehr erbringen. Es ist sehr wichtig, anhand von Objektivleistungskurven zu beurteilen, was ein Objektiv bei solch kurzen Wellenlängen realistisch leisten kann.
Bsp. 7: Theoretische Beschränkungen
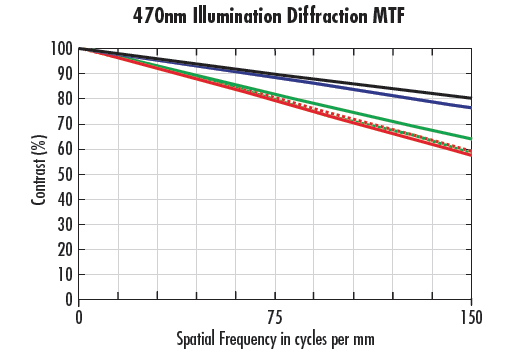
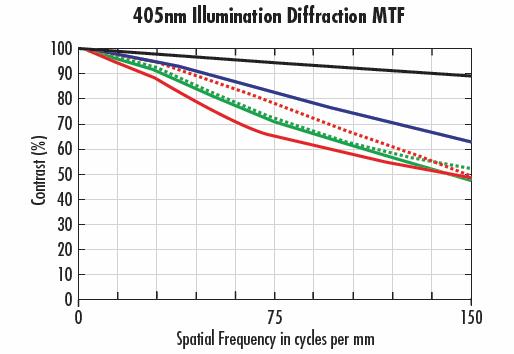
Abbildung 10 vergleicht ein Objektiv mit 35 mm Brennweite und f/2 bei blauer (470 nm) und violetter (405 nm) Beleuchtung (10a bzw. 10b). Abbildung 10a hat zwar eine niedrigere Beugungsgrenze, zeigt aber auch, dass die Wellenlänge 470 nm bei allen Feldpositionen eine höhere Leistung erbringt. Der Effekt wird hier verstärkt, wenn das Objektiv bei den für sein Design vorteilhaftesten Blendenzahlen und Arbeitsabständen verwendet wird (ausführlich in Die Modulationsübertragungsfunktion). Ein weiteres Wellenlängenproblem, das die Leistung stark beeinflussen kann, hängt mit der chromatischen Fokusverschiebung zusammen. Wenn der Wellenlängenbereich der Anwendung vergrößert wird, wird die Fähigkeit des Objektivs, ein hohes Leistungsniveau zu halten, beeinträchtigt. Der Abschnitt Aberrationen geht näher auf dieses Phänomen ein.













 Vorheriger Abschnitt
Vorheriger Abschnitt

















weitere regionale Telefonnummern
ANGEBOTSTOOL
Geben Sie zum Starten die Produktnummer ein.
Copyright 2023 | Edmund Optics, Ltd Unit 1, Opus Avenue, Nether Poppleton, York, YO26 6BL, UK
Die Edmund Optics GmbH Deutschland fungiert als Handelsvermittler für die Edmund Optics Ltd. in Großbritannien.
Vertragspartner ist die Edmund Optics Ltd. in Großbritannien.